Эйлер атындағы олимпиада, 2019-2020 оқу жылы, аймақтық кезеңнің 2 туры

Теңқабырғалы $ABC$ үшбұрышының $BC$ қабырғасына параллель орта сызығында $D$ нүктесі белгіленген. $BA$ қабырғасының $A$ нүктесінен ары созындысынан $\angle ECA = \angle DCA$ болатындай $E$, $CA$ қабырғасының $A$ нүктесінен ары созындысынан $\angle FBA = \angle DBA$ болатындай $F$ нүктесі алынған. $A$ нүктесі $DEF$ үшбұрышының $EF$ қабырғасына параллель болатын орта сызығында жататынын дәлелдеңіз. ( А. Кузнецов )

Комментарий/решение

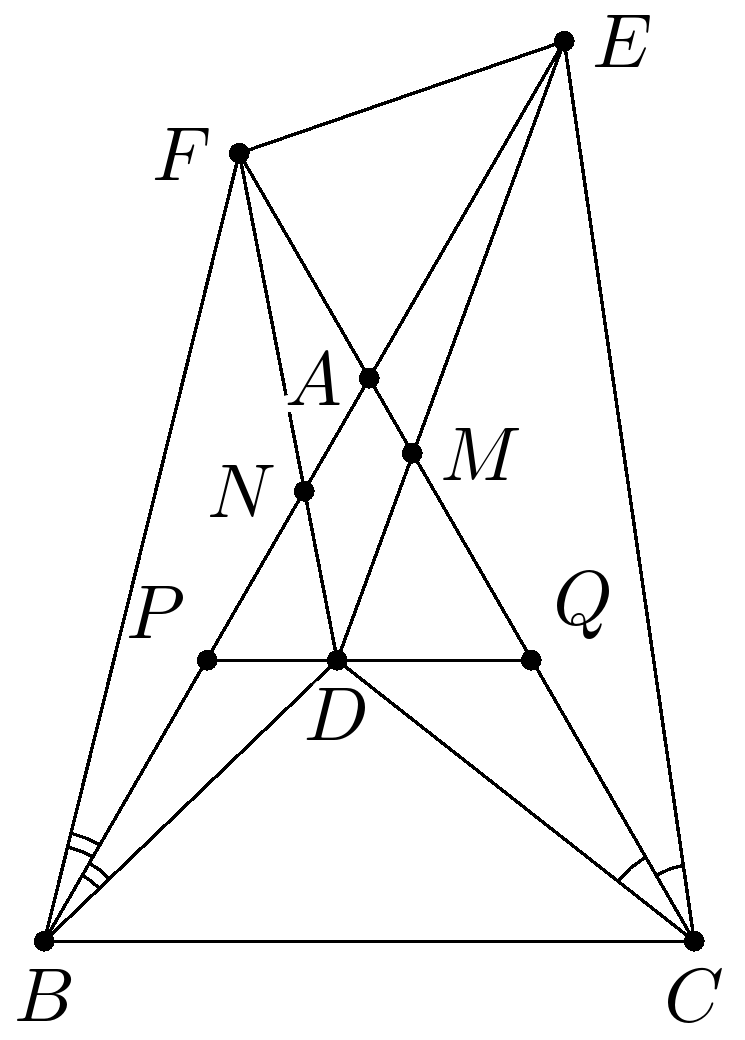
Комментарии от администратора Комментарии от администратора №1.     Обозначим через $P$ и $Q$ середины сторон $AB$ и $AC,$ а через $M$ и $N$ — точки, в которых $DE$ и $DF$ пересекают стороны $AC$ и $AB$ соответственно. Тогда треугольник $DPB$ будет подобен треугольнику $FAB$ по двум углам ($\angle DBP = \angle FBA$ по условию, $\angle BPD = \angle BAF = 120^\circ$) с коэффициентом 2, поскольку $AB = 2PB.$ Тогда по свойству биссектрисы $DN/NF = DB/BF = 1/2.$ Аналогично $DM/ME = 1/2.$ Следовательно, $S_{FAE} = 2S_{FDA}$ (так как сторона $AF$ у треугольников общая, а отношение опущенных на нее высот равно $DM/ME = 1/2$) и, аналогично, $S_{FAE} = 2S_{EDA},$ откуда $S_{FDE} = 2S_{FAE},$ и потому высота из вершины $A$ на $EF$ вдвое меньше высоты из вершины $D$ на $EF,$ откуда и вытекает утверждение задачи.