15-я Международная Жаутыковская олимпиада по математике, 2019 год

Дан равнобедренный треугольник $ABC$, $AC=BC$. На стороне $AC$ выбрана точка $D$. Окружность $S_1$ с радиусом $R$ и центром $O_1$ касается отрезка $AD$ и продолжений $BA$ и $BD$ за точки $A$ и $D$ соответственно. Окружность $S_2$ с радиусом $2R$ и центром $O_2$ касается отрезка $DC$ и продолжений $BD$ и $BC$ за точки $D$ и $C$ соответственно. Пусть касательная к описанной окружности треугольника $BO_1O_2$ в точке $O_2$ пересекает прямую $BA$ в точке $F$. Докажите, что $O_1F=O_1O_2$. ( И. Воронович )

Комментарий/решение

так как $O_{2}L, O_{1}G \perp AC$ и $O_{1}H \perp AB$ так как $O_{2}L=2O_{1}G$ тогда $O_{1}O_{2} = O_{1}L$ если $FO_{1} = O_{1}O_{2}=O_{1}L$ или $FH = GL$ что тоже самое что $\angle O_{1}FO_{2} = \dfrac{\angle ABC}{2}$ но тогда $\angle ALF = \dfrac{ \angle ABC}{2}$ , то есть докажем что $\angle O_{1}O_{2}F = \angle ALF$ пусть $ Q \in O_{1}O_{2} AC$ тогда $O_{1}O_{2}=QO_{1}=O_{1}L=X$ тогда возьмем на $AB$ такую точку $Y$ что $YO_{1}=X$ тогда $YH=GL$ и точки $Y,O_{2},L,Q$ лежат на окружности с радиусом $X$ откуда $\angle ALF = YO_{2}Q = \dfrac{\angle ABC}{2}$ но тогда $YO_{2}$ есть касательная значит $Y=F$ откуда $O_{1}F=O_{1}O_{2}$

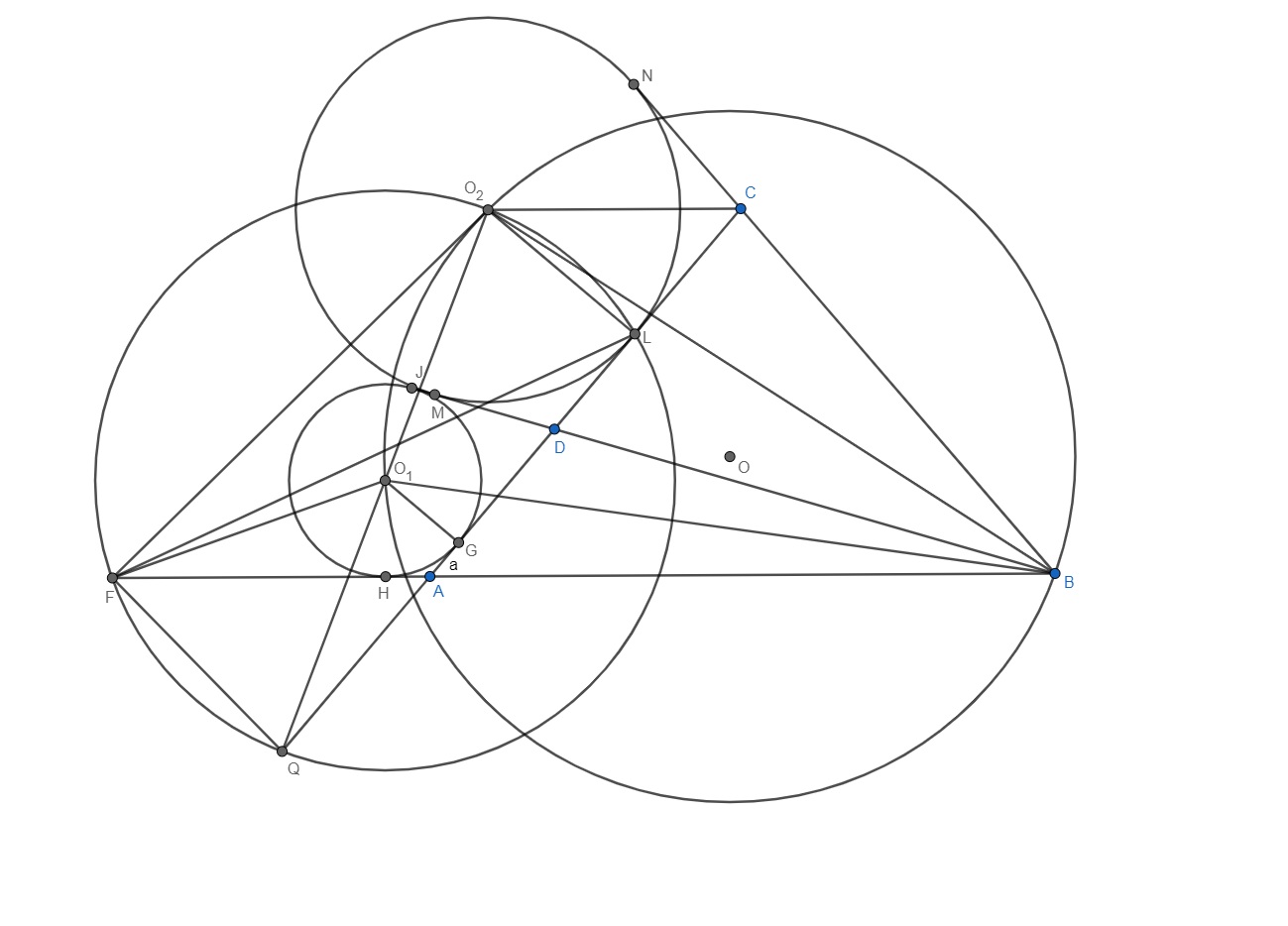
$O_1O_2 \cap AC=X$

Заметим что $X$ является центром гомотетии для $S_1, S_2$. Отсюда $\dfrac{XO_1}{XO_2}=\dfrac{R}{2R}=\dfrac{1}{2} \Longrightarrow XO_1=O_1O_2$

Пусть $(AO_1X) \cap AB=F’$, тогда $\angle XAF’=\angle XO_1F’=\angle B$ и $O_1F’=O_1X=O_1O_2 \Longrightarrow \angle XO_1F’=2 \cdot \angle XO_2F’=\angle B=2 \cdot \angle XO_2F \Longrightarrow F’=F$