14-я Жаутыковская олимпиада (2018), теоретический тур
Оптика движущихся сред (10,0 балла)
Часть 1. Четырехмерные векторы.
Рассмотрим две инерциальные системы отсчета $S$ и $S'$, из которых вторая движется относительно первой со скоростью $V$ как показано на рисунке. Будем считать, что начала $O$ и $O'$ совпадают в начальный момент времени $t=t'=0$ по часам обеих систем отсчета $S$ и $S'$. Известно, что преобразования Лоренца пространственно-временных координат любого события $(x',y',z',ct')$ в системе $S'$ в пространственно-временные координаты $(x,y,z,ct)$ этого же события в системе $S$ имеют вид $$x=\frac{x'+(V/c)ct'}{\sqrt{1-V^2/c^2}}, y=y', z=z', ct=\frac{ct'+(V/c)x'}{\sqrt{1-V^2/c^2}},$$ где $c=2,9979\cdot 10^8$ м/с — скорость света.
В формулах преобразований Лоренца пространственные координаты и время специально приведены к одинаковой размерности, так как они вместе образуют так называемый $4$-вектор. Известно, что компоненты всех $4$-векторов преобразуются одинаковым образом при переходе из одной инерциальной системы отсчета в другую. В частности, 4-вектор образуют компоненты импульса и энергия.
Пусть в системе отсчета $S$ движется объект, который имеет полную энергию $E$ и проекции импульса на оси координат $OX$, $OY$ и $OZ$ равные соответственно $p_x$, $p_y$, $p_z$.
1.1. Запишите преобразования энергии и импульса объекта из системы $S$ в систему $S'$. Пусть некоторый объект движется в системе отсчет $S$, имея полную энергию $E$, импульс $p$ и массу покоя $m$. При преобразовании его энергии и импульса из одной системы отсчета в другую величина $E^2-p^2 c^2=\text{inv}$ остается инвариантной.
1.2. Выразите инвариант $\text{inv}$ через $m$ и $c$.
Часть 2. Эффект Доплера и аберрация света. Пусть в системе отсчета $S$ в плоскости $XY$ распространяется электромагнитная волна (ЭМВ) с частотой $\omega$ так, что ее направление составляет угол $\varphi$ с осью $OX$.
2.1. Найдите частоту $\omega'$ ЭМВ, которую зафиксирует наблюдатель в системе отсчета $S'$.
2.2. Найдите угол $\varphi'$, который составляет направление распространения ЭМВ в системе отсчета $S'$ с осью $O'X'$.
Астрономические наблюдения показали, что положение вновь открытой массивной звезды $X$ на небесной сфере (то есть по отношению к очень удаленным объектам) не остается постоянным в течение года. Оно описывает эллипс с отношением полуосей $0,9$. Эклиптической широтой звезды называется угол между направлением на звезду и плоскостью эклиптики, которую можно считать совпадающей с плоскостью орбиты движения Земли вокруг Солнца.
2.3. Найдите эклиптическую широту $\delta$ звезды $X$ в градусах.
Наблюдение за спектром излучения звезды $X$ показали, что частоты длин волн сдвинуты в красную область. Относительное изменение частоты регистрируемого излучения составляет $(\Delta\omega/\omega)_0=9,9945\cdot 10^{-3}$. Из независимого эксперимента установили, что скорость удаления звезды $X$ от Солнца равна $\vartheta_x=\frac{1}{100}c$.
2.4. Найдите и рассчитайте вторую космическую скорость $\vartheta_II$ на поверхности звезды $X$.
Часть 3. Свет в движущейся среде.
Рассмотрим те же две системы отсчета, что и в Части 1. Пусть в системе отсчета в плоскости $X'Y'$ движется объект, скорость которого имеет проекции $u_{x}'$ на ось $O'X'$ и $u_{y}'$ на ось $O'Y'$ соответственно.
3.1. Найдите проекции скорости объекта $u_{x}$ на ось $OX$ и $u_{y}$ на ось $OY$ в системе отсчета $S$.
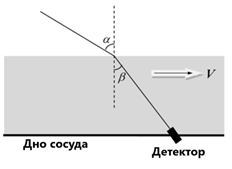
Рассмотрим поток воды, движущийся относительно дна сосуда со скоростью $V$. На поверхность воды падает плоская электромагнитная волна, которая составляет угол $\alpha$ с нормалью в лабораторной системе отсчета. На дне сосуда установлен остронаправленный детектор. Считайте коэффициент преломления воды известным и равным $n$.
При скорости воды $V\ll c$, выражение для синуса угла $\beta$, под которым детектор фиксирует излучение, имеет вид $$\sin(\beta)=A_1+B_1 V.$$
3.2. Найдите $A_1$, $B_1$ и выразите их через $\alpha$ и $n$. При скорости воды $V\ll c$, выражение для скорости излучения $\vartheta_{m}$ в лабораторной системе отсчета имеет вид $$\vartheta_{m}=A_2+B_2 V.$$
3.3. Найдите $A_2$, $B_2$ и выразите их через $\beta$, $n$, $c$.
3.4. Найдите число полос $\Delta N$, на которое сместится интерференционная картина при изменении скорости жидкости от $0$ до $\vartheta$, и выразите его через $L$, $n$, $\vartheta$, $c$, и $\lambda$.
В реальном опыте было получено значение $\Delta N=0,23$ при $L=1,49$ м, $\vartheta=7,06$ м/с и $\lambda=536$ нм.
3.5. Определите по этим данным показатель преломления воды $n$.
Математическая подсказка
Вам может понадобится знание следующего приближенного равенства: $$(1+x)^{\alpha} \thickapprox 1+\alpha x, при x\ll 1.$$
посмотреть в олимпиаде
Часть 1. Четырехмерные векторы.
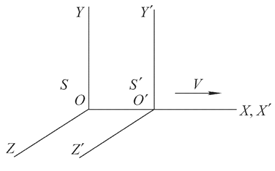
Рассмотрим две инерциальные системы отсчета $S$ и $S'$, из которых вторая движется относительно первой со скоростью $V$ как показано на рисунке. Будем считать, что начала $O$ и $O'$ совпадают в начальный момент времени $t=t'=0$ по часам обеих систем отсчета $S$ и $S'$. Известно, что преобразования Лоренца пространственно-временных координат любого события $(x',y',z',ct')$ в системе $S'$ в пространственно-временные координаты $(x,y,z,ct)$ этого же события в системе $S$ имеют вид $$x=\frac{x'+(V/c)ct'}{\sqrt{1-V^2/c^2}}, y=y', z=z', ct=\frac{ct'+(V/c)x'}{\sqrt{1-V^2/c^2}},$$ где $c=2,9979\cdot 10^8$ м/с — скорость света.
В формулах преобразований Лоренца пространственные координаты и время специально приведены к одинаковой размерности, так как они вместе образуют так называемый $4$-вектор. Известно, что компоненты всех $4$-векторов преобразуются одинаковым образом при переходе из одной инерциальной системы отсчета в другую. В частности, 4-вектор образуют компоненты импульса и энергия.
Пусть в системе отсчета $S$ движется объект, который имеет полную энергию $E$ и проекции импульса на оси координат $OX$, $OY$ и $OZ$ равные соответственно $p_x$, $p_y$, $p_z$.
1.1. Запишите преобразования энергии и импульса объекта из системы $S$ в систему $S'$. Пусть некоторый объект движется в системе отсчет $S$, имея полную энергию $E$, импульс $p$ и массу покоя $m$. При преобразовании его энергии и импульса из одной системы отсчета в другую величина $E^2-p^2 c^2=\text{inv}$ остается инвариантной.
1.2. Выразите инвариант $\text{inv}$ через $m$ и $c$.
Часть 2. Эффект Доплера и аберрация света. Пусть в системе отсчета $S$ в плоскости $XY$ распространяется электромагнитная волна (ЭМВ) с частотой $\omega$ так, что ее направление составляет угол $\varphi$ с осью $OX$.
2.1. Найдите частоту $\omega'$ ЭМВ, которую зафиксирует наблюдатель в системе отсчета $S'$.
2.2. Найдите угол $\varphi'$, который составляет направление распространения ЭМВ в системе отсчета $S'$ с осью $O'X'$.
Астрономические наблюдения показали, что положение вновь открытой массивной звезды $X$ на небесной сфере (то есть по отношению к очень удаленным объектам) не остается постоянным в течение года. Оно описывает эллипс с отношением полуосей $0,9$. Эклиптической широтой звезды называется угол между направлением на звезду и плоскостью эклиптики, которую можно считать совпадающей с плоскостью орбиты движения Земли вокруг Солнца.
2.3. Найдите эклиптическую широту $\delta$ звезды $X$ в градусах.
Наблюдение за спектром излучения звезды $X$ показали, что частоты длин волн сдвинуты в красную область. Относительное изменение частоты регистрируемого излучения составляет $(\Delta\omega/\omega)_0=9,9945\cdot 10^{-3}$. Из независимого эксперимента установили, что скорость удаления звезды $X$ от Солнца равна $\vartheta_x=\frac{1}{100}c$.
2.4. Найдите и рассчитайте вторую космическую скорость $\vartheta_II$ на поверхности звезды $X$.
Часть 3. Свет в движущейся среде.
Рассмотрим те же две системы отсчета, что и в Части 1. Пусть в системе отсчета в плоскости $X'Y'$ движется объект, скорость которого имеет проекции $u_{x}'$ на ось $O'X'$ и $u_{y}'$ на ось $O'Y'$ соответственно.
3.1. Найдите проекции скорости объекта $u_{x}$ на ось $OX$ и $u_{y}$ на ось $OY$ в системе отсчета $S$.
Рассмотрим поток воды, движущийся относительно дна сосуда со скоростью $V$. На поверхность воды падает плоская электромагнитная волна, которая составляет угол $\alpha$ с нормалью в лабораторной системе отсчета. На дне сосуда установлен остронаправленный детектор. Считайте коэффициент преломления воды известным и равным $n$.
При скорости воды $V\ll c$, выражение для синуса угла $\beta$, под которым детектор фиксирует излучение, имеет вид $$\sin(\beta)=A_1+B_1 V.$$
3.2. Найдите $A_1$, $B_1$ и выразите их через $\alpha$ и $n$. При скорости воды $V\ll c$, выражение для скорости излучения $\vartheta_{m}$ в лабораторной системе отсчета имеет вид $$\vartheta_{m}=A_2+B_2 V.$$
3.3. Найдите $A_2$, $B_2$ и выразите их через $\beta$, $n$, $c$.
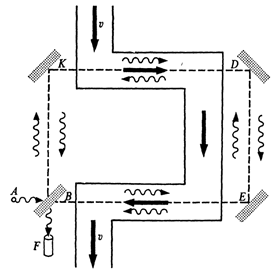
3.4. Найдите число полос $\Delta N$, на которое сместится интерференционная картина при изменении скорости жидкости от $0$ до $\vartheta$, и выразите его через $L$, $n$, $\vartheta$, $c$, и $\lambda$.
В реальном опыте было получено значение $\Delta N=0,23$ при $L=1,49$ м, $\vartheta=7,06$ м/с и $\lambda=536$ нм.
3.5. Определите по этим данным показатель преломления воды $n$.
Математическая подсказка
Вам может понадобится знание следующего приближенного равенства: $$(1+x)^{\alpha} \thickapprox 1+\alpha x, при x\ll 1.$$
Комментарий/решение:
Возможно, что при неправильном наборе формул, они будут
доредактированы модератором. При этом содержание не будет меняться.