14-я Жаутыковская олимпиада (2018), теоретический тур
Задача №1. (10,0 балла)
Эта задача состоит из трех частей, не связанных друг с другом.
Задача А (3,0 балла).
А1. Узкая цилиндрическая пробирка со смещенным центром масс плавает вертикально в воде в очень широком сосуде. В состоянии равновесия пробирка погружена в воду на глубину $h_0$. Площадь поперечного сечения пробирки равна $S_0$. Определите период малых вертикальных колебаний пробирки.
А2. Пробирку помещают в цилиндрический сосуд с площадью поперечного сечения $S$, заполненный водой. Пробирка совершает малые колебания вдоль оси сосуда.
А2.1. Пробирка опустилась на малую величину $x$. Выразите изменение потенциальной энергии системы через $x$, глубину погружения $h_0$, площади сечений $S_0$, $S$, плотность воды $\rho$ и ускорение свободного падения $g$.
А2.2. Вблизи положения равновесия скорость пробирки равна $\vartheta_0$. Выразите кинетическую энергию системы через скорость пробирки $\vartheta_0$, глубину погружения $h_0$, площади сечений $S_0$, $S$, плотность воды $\rho$. Считайте, что в зазоре между пробиркой и стенками сосуда вся жидкость движется с одинаковой скоростью $\vartheta$.
А2.3. Найдите период колебаний пробирки в сосуде.
Задача В (4,0 балла). Изображённая на рисунке схема состоит из конденсатора ёмкостью $С = 100$ мкФ, идеального диода, источника постоянного напряжения $U=10$ В, трёх одинаковых резисторов сопротивлением $R=10$ кОм и ключа. В начальный момент конденсатор не заряжен, ключ разомкнут. После замыкания ключа ток через диод идёт в течение времени $\tau=462$ мс, а затем прекращается.
1. Найдите ток через диод сразу после замыкания ключа;
2. Найдите полный заряд, протекший через диод.
Задача С (3,0 балла).
комментарий/решение
Эта задача состоит из трех частей, не связанных друг с другом.
Задача А (3,0 балла).
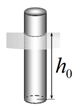
А1. Узкая цилиндрическая пробирка со смещенным центром масс плавает вертикально в воде в очень широком сосуде. В состоянии равновесия пробирка погружена в воду на глубину $h_0$. Площадь поперечного сечения пробирки равна $S_0$. Определите период малых вертикальных колебаний пробирки.
А2. Пробирку помещают в цилиндрический сосуд с площадью поперечного сечения $S$, заполненный водой. Пробирка совершает малые колебания вдоль оси сосуда.
А2.1. Пробирка опустилась на малую величину $x$. Выразите изменение потенциальной энергии системы через $x$, глубину погружения $h_0$, площади сечений $S_0$, $S$, плотность воды $\rho$ и ускорение свободного падения $g$.
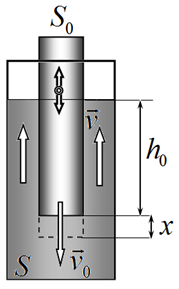
А2.2. Вблизи положения равновесия скорость пробирки равна $\vartheta_0$. Выразите кинетическую энергию системы через скорость пробирки $\vartheta_0$, глубину погружения $h_0$, площади сечений $S_0$, $S$, плотность воды $\rho$. Считайте, что в зазоре между пробиркой и стенками сосуда вся жидкость движется с одинаковой скоростью $\vartheta$.
А2.3. Найдите период колебаний пробирки в сосуде.
Задача В (4,0 балла). Изображённая на рисунке схема состоит из конденсатора ёмкостью $С = 100$ мкФ, идеального диода, источника постоянного напряжения $U=10$ В, трёх одинаковых резисторов сопротивлением $R=10$ кОм и ключа. В начальный момент конденсатор не заряжен, ключ разомкнут. После замыкания ключа ток через диод идёт в течение времени $\tau=462$ мс, а затем прекращается.
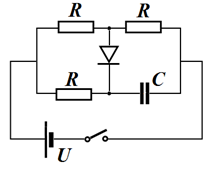
1. Найдите ток через диод сразу после замыкания ключа;
2. Найдите полный заряд, протекший через диод.
Задача С (3,0 балла).
комментарий/решение
Задача №2. (10,0 балла)
Физика в горах
Атмосфера реальной планеты, такой как Земля, имеет довольно сложное строение ввиду большого многообразия участвующих в ее формировании процессов и явлений. В этой задаче мы рассмотрим две простые модели нижнего слоя атмосферы, называемого тропосферой, который простирается на высоту до $10-15$ км над поверхностью Земли. Для понимания физики некоторых явлений достаточно считать атмосферу Земли состоящей из однокомпонентного двухатомного газа, имеющего молярную массу $\mu_{\text{air}}=28,9\cdot 10^{-3}$ кг/моль.
Часть 1. Изотермическая атмосфера. В атмосфере самый нижний приповерхностный слой имеет практически постоянную температуру, так как он нагревается от поверхности Земли. Поэтому примем в этой части, что температура атмосферы одинакова по всей ее высоте и равна $T_0=293$ К, а давление воздуха у поверхности Земли составляет $p_0=1,013\cdot 10^5$ Па. Считайте, что ускорение свободного падения $g=9,81$ м/с$^2$ не зависит от высоты над поверхностью Земли, так как толщина атмосферы много меньше радиуса Земли $R_{E}=6400$ км. Универсальная газовая постоянная равна $R=8,31$ Дж/(моль$\cdot$К).
1.1. Найдите и вычислите массу $M$ атмосферы Земли;
1.2. Найдите и вычислите давление воздуха $p_{H}$ на высоте $H=1500$ м над поверхностью Земли.
С физической точки зрения интересен вопрос о том, как быстро успевает прогреваться атмосфера при смене дня и ночи. Из наблюдений известна так называемая солнечная постоянная $\alpha=1367$ Вт/м$^2$, которая представляет собой суммарную мощность солнечного излучения в районе орбиты Земли, проходящего через единицу поверхности, ориентированной перпендикулярно его потоку.
1.3. Оцените количество теплоты $\sigma Q$, необходимое для нагревания атмосферы на $\Delta T=1$ К;
1.4. Найдите и вычислите интервал времени $\tau$, который должно светить Солнце, чтобы сообщить Земле количество теплоты $\sigma Q$.
Часть 2. Адиабатическая атмосфера. Реальная тропосфера не является изотермической и температура воздуха уменьшается с высотой. Благодаря постоянно протекающим конвективным процессам, тропосфера может считаться практически адиабатической. Пусть температура и давление воздуха у поверхности Земли составляют $T_0=293$ К и $p_0=1,013\cdot 10^5$ Па соответственно. По-прежнему считайте, что ускорение свободного падения $g=9,81$ м/с$^2$ не зависит от высоты над поверхностью Земли.
2.1. Найдите и вычислите температуру воздуха $T_{H}$ на высоте $H=1500$ м над поверхностью Земли;
2.2. Найдите и вычислите давление воздуха $p_{H}$ на высоте $H=1500$ м над поверхностью Земли.
В построенной модели высота тропосферы Земли определяется достижением некоторой критической температуры, при которой начинают играть существенную роль другие физические процессы.
2.3. Оцените разницу высот $\Delta H_{\text{atm}}$ тропосферы Земли в дневное и ночное время, если колебание температуры у поверхности за это время составляет $\Delta T_{\text{dn}}=20$ К.
Альпинист начинает восхождение на достаточно высокую гору, у подножия которой температура и давление воздуха равны $T_0=293$ К и $p_0=1,013\cdot 10^5$ Па. На высоте $H=1500$ м он решает сделать привал для того, чтобы вскипятить воду и обнаруживает, что она закипает быстрее обычного. Он открывает имеющийся при себе справочник по физике и находит, что при температуре $T_1=373$ К давление насыщенного водяного пара равно $p_1=p_0=1,013\cdot 10^5$ Па, а при температуре $T_2=365$ К — $p_2=0,757\cdot 10^5$ Па.
2.4. Найдите и вычислите температуру кипения воды на высоте $H=1500$ м.
После возобновления подъема альпинист обнаруживает, что на некоторой высоте появляется снег и приходится использовать специальное оборудование;
2.5. Найдите и вычислите высоту $h_0$, на которой альпинист заметил появление снежного покрова на горе.
Альпинист вспомнил разговор с местными жителями перед восхождением, в котором ему сообщили, что снежный покров полностью исчезает с горы при температуре у подножия, превышающей $T=310$ К.
2.6. Найдите и вычислите высоту $H_0$ горы, на которую совершает восхождение альпинист.
Поднявшись еще выше по склону горы на некоторую высоту $H'$, альпинист замечает появление тумана. Оглянувшись по сторонам, он отмечает, что облаков нет и ветер отсутствует. Альпинист знает, что молярная масса воды составляет $\mu_{H_2 O}=18\cdot 10^{-3}$ кг/моль, а по прогнозу погоды относительная влажность воздуха у подножия горы составляла $\varphi=0,25$. В справочнике по физике он находит формулу для давления насыщенных паров воды в интервале температур $T\in (250,300)$ К, которая имеет следующий вид $$\ln\frac{p_{\text{vap}}}{p_{\text{vap}0}}=a+b\ln\frac{T}{T_0},$$ где $p_{\text{vap}}$ — давление насыщенных паров при температуре $T$, $p_{\text{vap}0}$ — давление насыщенных паров при температуре $T_0$, $a=3,63\cdot 10^{-2}$, $b=18,2$ — постоянные. При вычислениях считайте, что пар находится в термодинамическом равновесии с окружающим его воздухом.
2.7. Найдите и вычислите высоту $H'$;
2.8. Найдите и вычислите минимальную влажность воздуха $\varphi_{\min}$ у подножья горы, при которой на ней еще будет наблюдаться туман.
Математическая подсказка Вам может понадобится знание следующего интеграла:$\int\frac{dx}{ax+b}=\frac{1}{a}\ln|ax+b|$.
комментарий/решение
Физика в горах

Атмосфера реальной планеты, такой как Земля, имеет довольно сложное строение ввиду большого многообразия участвующих в ее формировании процессов и явлений. В этой задаче мы рассмотрим две простые модели нижнего слоя атмосферы, называемого тропосферой, который простирается на высоту до $10-15$ км над поверхностью Земли. Для понимания физики некоторых явлений достаточно считать атмосферу Земли состоящей из однокомпонентного двухатомного газа, имеющего молярную массу $\mu_{\text{air}}=28,9\cdot 10^{-3}$ кг/моль.
Часть 1. Изотермическая атмосфера. В атмосфере самый нижний приповерхностный слой имеет практически постоянную температуру, так как он нагревается от поверхности Земли. Поэтому примем в этой части, что температура атмосферы одинакова по всей ее высоте и равна $T_0=293$ К, а давление воздуха у поверхности Земли составляет $p_0=1,013\cdot 10^5$ Па. Считайте, что ускорение свободного падения $g=9,81$ м/с$^2$ не зависит от высоты над поверхностью Земли, так как толщина атмосферы много меньше радиуса Земли $R_{E}=6400$ км. Универсальная газовая постоянная равна $R=8,31$ Дж/(моль$\cdot$К).
1.1. Найдите и вычислите массу $M$ атмосферы Земли;
1.2. Найдите и вычислите давление воздуха $p_{H}$ на высоте $H=1500$ м над поверхностью Земли.
С физической точки зрения интересен вопрос о том, как быстро успевает прогреваться атмосфера при смене дня и ночи. Из наблюдений известна так называемая солнечная постоянная $\alpha=1367$ Вт/м$^2$, которая представляет собой суммарную мощность солнечного излучения в районе орбиты Земли, проходящего через единицу поверхности, ориентированной перпендикулярно его потоку.
1.3. Оцените количество теплоты $\sigma Q$, необходимое для нагревания атмосферы на $\Delta T=1$ К;
1.4. Найдите и вычислите интервал времени $\tau$, который должно светить Солнце, чтобы сообщить Земле количество теплоты $\sigma Q$.
Часть 2. Адиабатическая атмосфера. Реальная тропосфера не является изотермической и температура воздуха уменьшается с высотой. Благодаря постоянно протекающим конвективным процессам, тропосфера может считаться практически адиабатической. Пусть температура и давление воздуха у поверхности Земли составляют $T_0=293$ К и $p_0=1,013\cdot 10^5$ Па соответственно. По-прежнему считайте, что ускорение свободного падения $g=9,81$ м/с$^2$ не зависит от высоты над поверхностью Земли.
2.1. Найдите и вычислите температуру воздуха $T_{H}$ на высоте $H=1500$ м над поверхностью Земли;
2.2. Найдите и вычислите давление воздуха $p_{H}$ на высоте $H=1500$ м над поверхностью Земли.
В построенной модели высота тропосферы Земли определяется достижением некоторой критической температуры, при которой начинают играть существенную роль другие физические процессы.
2.3. Оцените разницу высот $\Delta H_{\text{atm}}$ тропосферы Земли в дневное и ночное время, если колебание температуры у поверхности за это время составляет $\Delta T_{\text{dn}}=20$ К.
Альпинист начинает восхождение на достаточно высокую гору, у подножия которой температура и давление воздуха равны $T_0=293$ К и $p_0=1,013\cdot 10^5$ Па. На высоте $H=1500$ м он решает сделать привал для того, чтобы вскипятить воду и обнаруживает, что она закипает быстрее обычного. Он открывает имеющийся при себе справочник по физике и находит, что при температуре $T_1=373$ К давление насыщенного водяного пара равно $p_1=p_0=1,013\cdot 10^5$ Па, а при температуре $T_2=365$ К — $p_2=0,757\cdot 10^5$ Па.
2.4. Найдите и вычислите температуру кипения воды на высоте $H=1500$ м.
После возобновления подъема альпинист обнаруживает, что на некоторой высоте появляется снег и приходится использовать специальное оборудование;
2.5. Найдите и вычислите высоту $h_0$, на которой альпинист заметил появление снежного покрова на горе.
Альпинист вспомнил разговор с местными жителями перед восхождением, в котором ему сообщили, что снежный покров полностью исчезает с горы при температуре у подножия, превышающей $T=310$ К.
2.6. Найдите и вычислите высоту $H_0$ горы, на которую совершает восхождение альпинист.
Поднявшись еще выше по склону горы на некоторую высоту $H'$, альпинист замечает появление тумана. Оглянувшись по сторонам, он отмечает, что облаков нет и ветер отсутствует. Альпинист знает, что молярная масса воды составляет $\mu_{H_2 O}=18\cdot 10^{-3}$ кг/моль, а по прогнозу погоды относительная влажность воздуха у подножия горы составляла $\varphi=0,25$. В справочнике по физике он находит формулу для давления насыщенных паров воды в интервале температур $T\in (250,300)$ К, которая имеет следующий вид $$\ln\frac{p_{\text{vap}}}{p_{\text{vap}0}}=a+b\ln\frac{T}{T_0},$$ где $p_{\text{vap}}$ — давление насыщенных паров при температуре $T$, $p_{\text{vap}0}$ — давление насыщенных паров при температуре $T_0$, $a=3,63\cdot 10^{-2}$, $b=18,2$ — постоянные. При вычислениях считайте, что пар находится в термодинамическом равновесии с окружающим его воздухом.
2.7. Найдите и вычислите высоту $H'$;
2.8. Найдите и вычислите минимальную влажность воздуха $\varphi_{\min}$ у подножья горы, при которой на ней еще будет наблюдаться туман.
Математическая подсказка Вам может понадобится знание следующего интеграла:$\int\frac{dx}{ax+b}=\frac{1}{a}\ln|ax+b|$.
комментарий/решение
Задача №3. Оптика движущихся сред (10,0 балла)
Часть 1. Четырехмерные векторы.
Рассмотрим две инерциальные системы отсчета $S$ и $S'$, из которых вторая движется относительно первой со скоростью $V$ как показано на рисунке. Будем считать, что начала $O$ и $O'$ совпадают в начальный момент времени $t=t'=0$ по часам обеих систем отсчета $S$ и $S'$. Известно, что преобразования Лоренца пространственно-временных координат любого события $(x',y',z',ct')$ в системе $S'$ в пространственно-временные координаты $(x,y,z,ct)$ этого же события в системе $S$ имеют вид $$x=\frac{x'+(V/c)ct'}{\sqrt{1-V^2/c^2}}, y=y', z=z', ct=\frac{ct'+(V/c)x'}{\sqrt{1-V^2/c^2}},$$ где $c=2,9979\cdot 10^8$ м/с — скорость света.
В формулах преобразований Лоренца пространственные координаты и время специально приведены к одинаковой размерности, так как они вместе образуют так называемый $4$-вектор. Известно, что компоненты всех $4$-векторов преобразуются одинаковым образом при переходе из одной инерциальной системы отсчета в другую. В частности, 4-вектор образуют компоненты импульса и энергия.
Пусть в системе отсчета $S$ движется объект, который имеет полную энергию $E$ и проекции импульса на оси координат $OX$, $OY$ и $OZ$ равные соответственно $p_x$, $p_y$, $p_z$.
1.1. Запишите преобразования энергии и импульса объекта из системы $S$ в систему $S'$. Пусть некоторый объект движется в системе отсчет $S$, имея полную энергию $E$, импульс $p$ и массу покоя $m$. При преобразовании его энергии и импульса из одной системы отсчета в другую величина $E^2-p^2 c^2=\text{inv}$ остается инвариантной.
1.2. Выразите инвариант $\text{inv}$ через $m$ и $c$.
Часть 2. Эффект Доплера и аберрация света. Пусть в системе отсчета $S$ в плоскости $XY$ распространяется электромагнитная волна (ЭМВ) с частотой $\omega$ так, что ее направление составляет угол $\varphi$ с осью $OX$.
2.1. Найдите частоту $\omega'$ ЭМВ, которую зафиксирует наблюдатель в системе отсчета $S'$.
2.2. Найдите угол $\varphi'$, который составляет направление распространения ЭМВ в системе отсчета $S'$ с осью $O'X'$.
Астрономические наблюдения показали, что положение вновь открытой массивной звезды $X$ на небесной сфере (то есть по отношению к очень удаленным объектам) не остается постоянным в течение года. Оно описывает эллипс с отношением полуосей $0,9$. Эклиптической широтой звезды называется угол между направлением на звезду и плоскостью эклиптики, которую можно считать совпадающей с плоскостью орбиты движения Земли вокруг Солнца.
2.3. Найдите эклиптическую широту $\delta$ звезды $X$ в градусах.
Наблюдение за спектром излучения звезды $X$ показали, что частоты длин волн сдвинуты в красную область. Относительное изменение частоты регистрируемого излучения составляет $(\Delta\omega/\omega)_0=9,9945\cdot 10^{-3}$. Из независимого эксперимента установили, что скорость удаления звезды $X$ от Солнца равна $\vartheta_x=\frac{1}{100}c$.
2.4. Найдите и рассчитайте вторую космическую скорость $\vartheta_II$ на поверхности звезды $X$.
Часть 3. Свет в движущейся среде.
Рассмотрим те же две системы отсчета, что и в Части 1. Пусть в системе отсчета в плоскости $X'Y'$ движется объект, скорость которого имеет проекции $u_{x}'$ на ось $O'X'$ и $u_{y}'$ на ось $O'Y'$ соответственно.
3.1. Найдите проекции скорости объекта $u_{x}$ на ось $OX$ и $u_{y}$ на ось $OY$ в системе отсчета $S$.
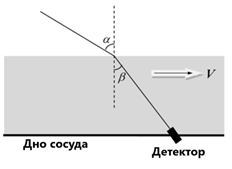
Рассмотрим поток воды, движущийся относительно дна сосуда со скоростью $V$. На поверхность воды падает плоская электромагнитная волна, которая составляет угол $\alpha$ с нормалью в лабораторной системе отсчета. На дне сосуда установлен остронаправленный детектор. Считайте коэффициент преломления воды известным и равным $n$.
При скорости воды $V\ll c$, выражение для синуса угла $\beta$, под которым детектор фиксирует излучение, имеет вид $$\sin(\beta)=A_1+B_1 V.$$
3.2. Найдите $A_1$, $B_1$ и выразите их через $\alpha$ и $n$. При скорости воды $V\ll c$, выражение для скорости излучения $\vartheta_{m}$ в лабораторной системе отсчета имеет вид $$\vartheta_{m}=A_2+B_2 V.$$
3.3. Найдите $A_2$, $B_2$ и выразите их через $\beta$, $n$, $c$.
3.4. Найдите число полос $\Delta N$, на которое сместится интерференционная картина при изменении скорости жидкости от $0$ до $\vartheta$, и выразите его через $L$, $n$, $\vartheta$, $c$, и $\lambda$.
В реальном опыте было получено значение $\Delta N=0,23$ при $L=1,49$ м, $\vartheta=7,06$ м/с и $\lambda=536$ нм.
3.5. Определите по этим данным показатель преломления воды $n$.
Математическая подсказка
Вам может понадобится знание следующего приближенного равенства: $$(1+x)^{\alpha} \thickapprox 1+\alpha x, при x\ll 1.$$
комментарий/решение
Часть 1. Четырехмерные векторы.
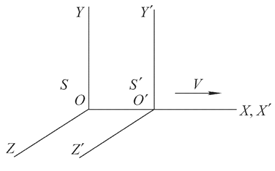
Рассмотрим две инерциальные системы отсчета $S$ и $S'$, из которых вторая движется относительно первой со скоростью $V$ как показано на рисунке. Будем считать, что начала $O$ и $O'$ совпадают в начальный момент времени $t=t'=0$ по часам обеих систем отсчета $S$ и $S'$. Известно, что преобразования Лоренца пространственно-временных координат любого события $(x',y',z',ct')$ в системе $S'$ в пространственно-временные координаты $(x,y,z,ct)$ этого же события в системе $S$ имеют вид $$x=\frac{x'+(V/c)ct'}{\sqrt{1-V^2/c^2}}, y=y', z=z', ct=\frac{ct'+(V/c)x'}{\sqrt{1-V^2/c^2}},$$ где $c=2,9979\cdot 10^8$ м/с — скорость света.
В формулах преобразований Лоренца пространственные координаты и время специально приведены к одинаковой размерности, так как они вместе образуют так называемый $4$-вектор. Известно, что компоненты всех $4$-векторов преобразуются одинаковым образом при переходе из одной инерциальной системы отсчета в другую. В частности, 4-вектор образуют компоненты импульса и энергия.
Пусть в системе отсчета $S$ движется объект, который имеет полную энергию $E$ и проекции импульса на оси координат $OX$, $OY$ и $OZ$ равные соответственно $p_x$, $p_y$, $p_z$.
1.1. Запишите преобразования энергии и импульса объекта из системы $S$ в систему $S'$. Пусть некоторый объект движется в системе отсчет $S$, имея полную энергию $E$, импульс $p$ и массу покоя $m$. При преобразовании его энергии и импульса из одной системы отсчета в другую величина $E^2-p^2 c^2=\text{inv}$ остается инвариантной.
1.2. Выразите инвариант $\text{inv}$ через $m$ и $c$.
Часть 2. Эффект Доплера и аберрация света. Пусть в системе отсчета $S$ в плоскости $XY$ распространяется электромагнитная волна (ЭМВ) с частотой $\omega$ так, что ее направление составляет угол $\varphi$ с осью $OX$.
2.1. Найдите частоту $\omega'$ ЭМВ, которую зафиксирует наблюдатель в системе отсчета $S'$.
2.2. Найдите угол $\varphi'$, который составляет направление распространения ЭМВ в системе отсчета $S'$ с осью $O'X'$.
Астрономические наблюдения показали, что положение вновь открытой массивной звезды $X$ на небесной сфере (то есть по отношению к очень удаленным объектам) не остается постоянным в течение года. Оно описывает эллипс с отношением полуосей $0,9$. Эклиптической широтой звезды называется угол между направлением на звезду и плоскостью эклиптики, которую можно считать совпадающей с плоскостью орбиты движения Земли вокруг Солнца.
2.3. Найдите эклиптическую широту $\delta$ звезды $X$ в градусах.
Наблюдение за спектром излучения звезды $X$ показали, что частоты длин волн сдвинуты в красную область. Относительное изменение частоты регистрируемого излучения составляет $(\Delta\omega/\omega)_0=9,9945\cdot 10^{-3}$. Из независимого эксперимента установили, что скорость удаления звезды $X$ от Солнца равна $\vartheta_x=\frac{1}{100}c$.
2.4. Найдите и рассчитайте вторую космическую скорость $\vartheta_II$ на поверхности звезды $X$.
Часть 3. Свет в движущейся среде.
Рассмотрим те же две системы отсчета, что и в Части 1. Пусть в системе отсчета в плоскости $X'Y'$ движется объект, скорость которого имеет проекции $u_{x}'$ на ось $O'X'$ и $u_{y}'$ на ось $O'Y'$ соответственно.
3.1. Найдите проекции скорости объекта $u_{x}$ на ось $OX$ и $u_{y}$ на ось $OY$ в системе отсчета $S$.
Рассмотрим поток воды, движущийся относительно дна сосуда со скоростью $V$. На поверхность воды падает плоская электромагнитная волна, которая составляет угол $\alpha$ с нормалью в лабораторной системе отсчета. На дне сосуда установлен остронаправленный детектор. Считайте коэффициент преломления воды известным и равным $n$.
При скорости воды $V\ll c$, выражение для синуса угла $\beta$, под которым детектор фиксирует излучение, имеет вид $$\sin(\beta)=A_1+B_1 V.$$
3.2. Найдите $A_1$, $B_1$ и выразите их через $\alpha$ и $n$. При скорости воды $V\ll c$, выражение для скорости излучения $\vartheta_{m}$ в лабораторной системе отсчета имеет вид $$\vartheta_{m}=A_2+B_2 V.$$
3.3. Найдите $A_2$, $B_2$ и выразите их через $\beta$, $n$, $c$.
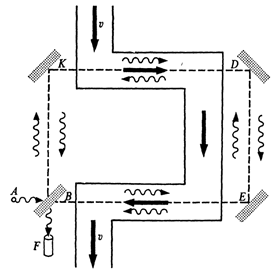
3.4. Найдите число полос $\Delta N$, на которое сместится интерференционная картина при изменении скорости жидкости от $0$ до $\vartheta$, и выразите его через $L$, $n$, $\vartheta$, $c$, и $\lambda$.
В реальном опыте было получено значение $\Delta N=0,23$ при $L=1,49$ м, $\vartheta=7,06$ м/с и $\lambda=536$ нм.
3.5. Определите по этим данным показатель преломления воды $n$.
Математическая подсказка
Вам может понадобится знание следующего приближенного равенства: $$(1+x)^{\alpha} \thickapprox 1+\alpha x, при x\ll 1.$$
комментарий/решение