14-я Жаутыковская олимпиада (2018), теоретический тур
(10,0 балла)
Эта задача состоит из трех частей, не связанных друг с другом.
Задача А (3,0 балла).
А1. Узкая цилиндрическая пробирка со смещенным центром масс плавает вертикально в воде в очень широком сосуде. В состоянии равновесия пробирка погружена в воду на глубину $h_0$. Площадь поперечного сечения пробирки равна $S_0$. Определите период малых вертикальных колебаний пробирки.
А2. Пробирку помещают в цилиндрический сосуд с площадью поперечного сечения $S$, заполненный водой. Пробирка совершает малые колебания вдоль оси сосуда.
А2.1. Пробирка опустилась на малую величину $x$. Выразите изменение потенциальной энергии системы через $x$, глубину погружения $h_0$, площади сечений $S_0$, $S$, плотность воды $\rho$ и ускорение свободного падения $g$.
А2.2. Вблизи положения равновесия скорость пробирки равна $\vartheta_0$. Выразите кинетическую энергию системы через скорость пробирки $\vartheta_0$, глубину погружения $h_0$, площади сечений $S_0$, $S$, плотность воды $\rho$. Считайте, что в зазоре между пробиркой и стенками сосуда вся жидкость движется с одинаковой скоростью $\vartheta$.
А2.3. Найдите период колебаний пробирки в сосуде.
Задача В (4,0 балла). Изображённая на рисунке схема состоит из конденсатора ёмкостью $С = 100$ мкФ, идеального диода, источника постоянного напряжения $U=10$ В, трёх одинаковых резисторов сопротивлением $R=10$ кОм и ключа. В начальный момент конденсатор не заряжен, ключ разомкнут. После замыкания ключа ток через диод идёт в течение времени $\tau=462$ мс, а затем прекращается.
1. Найдите ток через диод сразу после замыкания ключа;
2. Найдите полный заряд, протекший через диод.
Задача С (3,0 балла).
посмотреть в олимпиаде
Эта задача состоит из трех частей, не связанных друг с другом.
Задача А (3,0 балла).
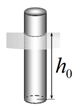
А1. Узкая цилиндрическая пробирка со смещенным центром масс плавает вертикально в воде в очень широком сосуде. В состоянии равновесия пробирка погружена в воду на глубину $h_0$. Площадь поперечного сечения пробирки равна $S_0$. Определите период малых вертикальных колебаний пробирки.
А2. Пробирку помещают в цилиндрический сосуд с площадью поперечного сечения $S$, заполненный водой. Пробирка совершает малые колебания вдоль оси сосуда.
А2.1. Пробирка опустилась на малую величину $x$. Выразите изменение потенциальной энергии системы через $x$, глубину погружения $h_0$, площади сечений $S_0$, $S$, плотность воды $\rho$ и ускорение свободного падения $g$.
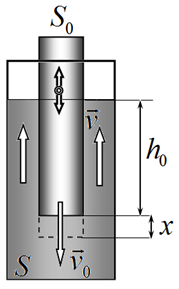
А2.2. Вблизи положения равновесия скорость пробирки равна $\vartheta_0$. Выразите кинетическую энергию системы через скорость пробирки $\vartheta_0$, глубину погружения $h_0$, площади сечений $S_0$, $S$, плотность воды $\rho$. Считайте, что в зазоре между пробиркой и стенками сосуда вся жидкость движется с одинаковой скоростью $\vartheta$.
А2.3. Найдите период колебаний пробирки в сосуде.
Задача В (4,0 балла). Изображённая на рисунке схема состоит из конденсатора ёмкостью $С = 100$ мкФ, идеального диода, источника постоянного напряжения $U=10$ В, трёх одинаковых резисторов сопротивлением $R=10$ кОм и ключа. В начальный момент конденсатор не заряжен, ключ разомкнут. После замыкания ключа ток через диод идёт в течение времени $\tau=462$ мс, а затем прекращается.
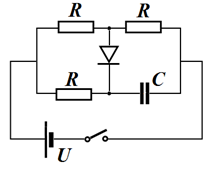
1. Найдите ток через диод сразу после замыкания ключа;
2. Найдите полный заряд, протекший через диод.
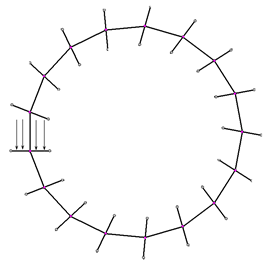
Задача С (3,0 балла).
Комментарий/решение:
Возможно, что при неправильном наборе формул, они будут
доредактированы модератором. При этом содержание не будет меняться.