11-я Жаутыковская олимпиада (2015), теоретический тур
Сосуд с водой (7 баллов)
1. [2,0 балла] Найдите высоту уровня воды в сосуде $x=x_0$ в тот момент, когда трубка будет полностью заполнена водой. Ответ выразите через $p_0$, $\rho$, $g$, $h$, $L$ и найдите его численное значение. Стенки сосуда и трубки покрывают материалом, который не проводит тепло. Воздуху внутри сосуда начинают сообщать тепло достаточно быстро, так что вода не успевает прогреваться.
2. [0,5 балла] Найдите зависимость давления воздуха в сосуде $p(x)$ как функцию от $x$. Ответ выразите через $p_0$, $\rho$, $g$, $L$, $x$.
3. [1,0 балла] Найдите зависимость температуры воздуха в сосуде $T(x)$ как функцию от $x$. Ответ выразите через $p_0$, $\rho$, $g$, $L$, $x$.
4. [1,0 балла] Найдите до какой температуры $T_m$ необходимо нагреть воздух, чтобы он полностью вытеснил воду из сосуда. Ответ выразите через $p_0$, $\rho$, $g$, $L$, $T_0$ и найдите его численное значение.
5. [2,5 балла] Найдите количество теплоты $Q$, которое надо сообщить воздуху, чтобы он полностью вытеснил воду из сосуда. Ответ выразите через $p_0$, $\rho$, $g$, $h$, $L$, $S$ и найдите его численное значение.
посмотреть в олимпиаде
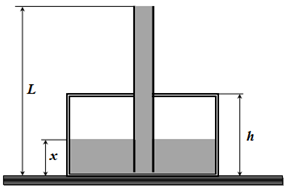
1. [2,0 балла] Найдите высоту уровня воды в сосуде $x=x_0$ в тот момент, когда трубка будет полностью заполнена водой. Ответ выразите через $p_0$, $\rho$, $g$, $h$, $L$ и найдите его численное значение. Стенки сосуда и трубки покрывают материалом, который не проводит тепло. Воздуху внутри сосуда начинают сообщать тепло достаточно быстро, так что вода не успевает прогреваться.
2. [0,5 балла] Найдите зависимость давления воздуха в сосуде $p(x)$ как функцию от $x$. Ответ выразите через $p_0$, $\rho$, $g$, $L$, $x$.
3. [1,0 балла] Найдите зависимость температуры воздуха в сосуде $T(x)$ как функцию от $x$. Ответ выразите через $p_0$, $\rho$, $g$, $L$, $x$.
4. [1,0 балла] Найдите до какой температуры $T_m$ необходимо нагреть воздух, чтобы он полностью вытеснил воду из сосуда. Ответ выразите через $p_0$, $\rho$, $g$, $L$, $T_0$ и найдите его численное значение.
5. [2,5 балла] Найдите количество теплоты $Q$, которое надо сообщить воздуху, чтобы он полностью вытеснил воду из сосуда. Ответ выразите через $p_0$, $\rho$, $g$, $h$, $L$, $S$ и найдите его численное значение.
Комментарий/решение:
Возможно, что при неправильном наборе формул, они будут
доредактированы модератором. При этом содержание не будет меняться.