8-я Жаутыковская олимпиада (2012), теоретический тур
(10 баллов)
Эта задача состоит из трех частей, не связанных друг с другом.
Задача 1.А. 2012 (4 балла)
Задача 1.В. И диоды $...$(2,5 балла)
Задача 1.С. Плоская линза (3,5 балла)
посмотреть в олимпиаде
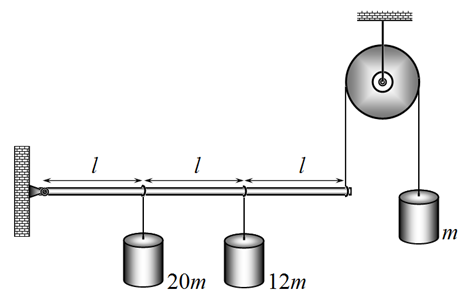
Задача 1.А. 2012 (4 балла)
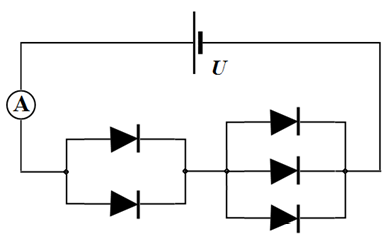
Задача 1.В. И диоды $...$(2,5 балла)
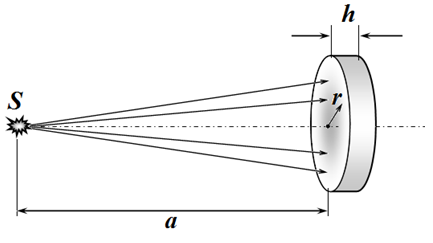
Задача 1.С. Плоская линза (3,5 балла)
Комментарий/решение:
Возможно, что при неправильном наборе формул, они будут
доредактированы модератором. При этом содержание не будет меняться.