4-я Жаутыковская олимпиада (2008), теоретический тур

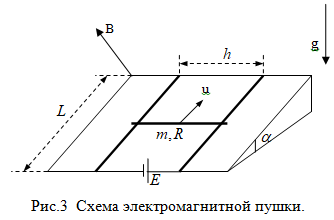
Электромагнитная пушка (10 баллов) Инженерами была предложена следующая конструкция электромагнитной пушки. На непроводящей плоскости с углом наклона $\alpha$ к горизонту на расстоянии $h$ друг от друга закреплены два не имеющих сопротивления проводника, по которым на скользящих контактах может перемещаться подвижный проводник массой $m$ и сопротивлением $R$ (см. Рис.3). Между нижними концами проводников включен источник питания с э.д.с. $E$ и нулевым внутренним сопротивлением, а система помещена в магнитное поле с индукцией $B$, перпендикулярное наклонной плоскости. Длина ребра плоскости равна $L$, а в начальный момент времени подвижный проводник покоится вблизи источника тока.

[label=\alph*)]
1. Определите минимальное значение э.д.с. $E_{\min}$, при котором проводник начинает движение вверх по плоскости; (1 балл)
2. При движении проводника по плоскости со временем устанавливается постоянная сила тока $I_0$. Найдите ее, считая что э.д.с. $E>E_{\min}$; (1 балл)
3. При перемещении проводника по плоскости со временем устанавливается постоянная скорость его движения $u_0$. Найдите ее, считая что э.д.с. $E>E_{\min}$; (2 балла)
4. При достаточно больших $L$ движение стержня перед отрывом можно считать установившимся. Тогда заряд $q$, прошедший через источник питания выражается формулой
$$q=C_1L+C_2.$$ Определите $C_1$ и $C_2$; (3 балла)
5. В условиях предыдущего пункта количество теплоты $Q$, выделившееся в проводнике к моменту отрыва, записывается в виде $$Q=C_3L+C_4.$$
Определите $C_3$ и $C_4$. (3 балла)

Примечание: В данной задаче Вы можете пренебречь трением и явлением самоиндукции.