4-я Жаутыковская олимпиада (2008), теоретический тур

Задача №1. Данная задача состоит из четырех независимых частей.
1А (2 балла).

В закрытом вертикальном цилиндрическом сосуде радиуса $R$ полностью заполненном водой находится однородный сплошной шар радиуса $R/2$. Сосуд раскрутили вокруг его вертикальной оси до угловой скорости $\omega$. Найдите силу давления шара на боковую поверхность цилиндра. Плотность воды — $\rho_0$, плотность материала шара — $\rho$.
1В (3 балла). Теплоемкости тел могут зависеть от температуры (например, при низких температурах). Два одинаковых тела, удельные теплоемкости которых зависят от температуры $t$ по закону $$c(t)=c_0(1+\alpha t),$$ (где $c_0$ и $\alpha$ — известные постоянные величины) приведены в тепловой контакт. Начальные температуры тел равны $t_1$ и $t_2$. Определите установившуюся температуру тел. Потерями теплоты пренебречь.
1C (2 балла).

Найдите период малых радиально симметричных колебаний кольца, состоящего из $n$ одинаковых коротких невесомых пружинок жёсткостью $k$, соединяющих $n$ точечных масс $m$ (см.Рис.1). Считайте, что $n\gg 1$.
1D (3 балла).

Тонкая плоско-параллельная стеклянная пластина с показателем преломления $n=1,5$ разрезана на две части, одна из которых представляет собой бипризму Френеля с малым преломляющим углом $\gamma=0,1$ рад. (см.Рис.2) Пластина облучается мощным пучком монохроматического излучения с интенсивностью $I=10$ кВт/см$^2$. Свет падает перпендикулярно плоскости пластины площадью $S=10$ см$^2$. Какую силу $F$ необходимо приложить, чтобы раздвинуть разрезанные части пластины так, чтобы между ними образовался небольшой зазор постоянной толщины? Потерями света в стекле и отражением на границах пренебречь.
комментарий/решение

---

Задача №2.  Электромагнитная пушка (10 баллов)
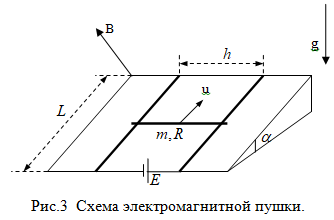
Инженерами была предложена следующая конструкция электромагнитной пушки. На непроводящей плоскости с углом наклона $\alpha$ к горизонту на расстоянии $h$ друг от друга закреплены два не имеющих сопротивления проводника, по которым на скользящих контактах может перемещаться подвижный проводник массой $m$ и сопротивлением $R$ (см. Рис.3). Между нижними концами проводников включен источник питания с э.д.с. $E$ и нулевым внутренним сопротивлением, а система помещена в магнитное поле с индукцией $B$, перпендикулярное наклонной плоскости. Длина ребра плоскости равна $L$, а в начальный момент времени подвижный проводник покоится вблизи источника тока.

1. Определите минимальное значение э.д.с. $E_{\min}$, при котором проводник начинает движение вверх по плоскости; (1 балл)
2. При движении проводника по плоскости со временем устанавливается постоянная сила тока $I_0$. Найдите ее, считая что э.д.с. $E>E_{\min}$; (1 балл)
3. При перемещении проводника по плоскости со временем устанавливается постоянная скорость его движения $u_0$. Найдите ее, считая что э.д.с. $E>E_{\min}$; (2 балла)
4. При достаточно больших $L$ движение стержня перед отрывом можно считать установившимся. Тогда заряд $q$, прошедший через источник питания выражается формулой
$$q=C_1L+C_2.$$ Определите $C_1$ и $C_2$; (3 балла)
5. В условиях предыдущего пункта количество теплоты $Q$, выделившееся в проводнике к моменту отрыва, записывается в виде $$Q=C_3L+C_4.$$
Определите $C_3$ и $C_4$. (3 балла)

Примечание: В данной задаче Вы можете пренебречь трением и явлением самоиндукции.
комментарий/решение

---

Задача №3. Атом гелия (10 баллов)
Атом гелия является простейшей многоэлектронной системой. Согласно планетарной модели атома он состоит из ядра с зарядом $+2e$ и двух электронов, которые двигаются вокруг него. Задача об атоме гелия в общем виде решается на основе квантовой механики, где учитывается тождественность (неразличимость) двух электронов. Это достаточно сложная задача. Однако, многие качественные сведения об атоме гелия можно получить не решая непосредственно квантовомеханическую задачу, а всего лишь применяя правила квантования Бора. В этой задаче Вам предлагается качественно исследовать атом гелия. В дальнейшем во всех ниже перечисленных пунктах считайте, что электроны в атоме имеют минимальную возможную энергию (находятся в основном состоянии) и двигаются по одной круговой орбите радиуса $r$. Согласно постулатам Бора орбитальный момент импульса каждого электрона равен целому числу постоянных Планка $\hbar$.

1. Напишите соотношение, которому должны удовлетворять импульс $p$ и радиус орбиты $r$ каждого электрона для основного состояния атома гелия; (1 балл)
2. Напишите выражение для потенциальной энергии системы как функцию $r$; (2 балла)
3. Определите выражение для радиуса орбиты электронов $r$ и найдите его численное значение; (2 балла)
4. Определите выражение для полной энергии основного состояния атома гелия и найдите ее численное значение; (1 балл)
5. Определите выражение для энергии однократной ионизации атома гелия и найдите ее численное значение; (2 балл)
Атомы могут ионизироваться под действием внешнего давления. Такое явление происходит в центрах массивных планет.
6. Оцените давление, при котором произойдет ионизация атомов гелия; (2 балла)

комментарий/решение

---