4-я Жаутыковская олимпиада (2008), теоретический тур
Данная задача состоит из четырех независимых частей.
1А (2 балла).
1В (3 балла). Теплоемкости тел могут зависеть от температуры (например, при низких температурах). Два одинаковых тела, удельные теплоемкости которых зависят от температуры $t$ по закону $$c(t)=c_0(1+\alpha t),$$ (где $c_0$ и $\alpha$ — известные постоянные величины) приведены в тепловой контакт. Начальные температуры тел равны $t_1$ и $t_2$. Определите установившуюся температуру тел. Потерями теплоты пренебречь.
1C (2 балла).
1D (3 балла).
посмотреть в олимпиаде
1А (2 балла).
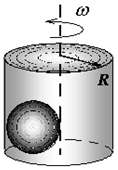
1В (3 балла). Теплоемкости тел могут зависеть от температуры (например, при низких температурах). Два одинаковых тела, удельные теплоемкости которых зависят от температуры $t$ по закону $$c(t)=c_0(1+\alpha t),$$ (где $c_0$ и $\alpha$ — известные постоянные величины) приведены в тепловой контакт. Начальные температуры тел равны $t_1$ и $t_2$. Определите установившуюся температуру тел. Потерями теплоты пренебречь.
1C (2 балла).
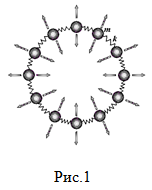
1D (3 балла).
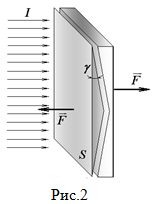
Комментарий/решение:
Возможно, что при неправильном наборе формул, они будут
доредактированы модератором. При этом содержание не будет меняться.