Олимпиада Туймаада по математике. Старшая лига. 2018 год

Четырехугольник $ABCD$, диагонали которого перпендикулярны, вписан в окружность с центром в точке $O$. Касательные к этой окружности в точках $A$ и $C$ вместе с прямой $BD$ образуют треугольник $\Delta$. Докажите, что описанные окружности треугольников $BOD$ и $\Delta$ касаются. ( А. Кузнецов )

Комментарий/решение

Пусть $w$ окружность описанная около $ABCD$ и пусть касательные пересекаются в точке $F$ и $H \in AC \cap BD, \ AC \perp BD$ так же $E \in BD \cap AF, \ G \in BD \cap CF$ пусть $w_{1}$ окружность описанная около $BOD$ и $w_{2}$ около $GEF$ так же пусть $F'$ середина $AC$ так как $AF,CF$ касательные или $OF' \cdot OF = AF^2 = CF^2$ тогда при инверсии относительно $w$ касательные $AF,CF$ переходят в окружности $X,Y$ описанные около треугольников $OF'A, OF'C$ соответственно, так же, так как $w_{1}$ проходит через центр $w$ тогда при инверсии относительно $w$ окр-сть $w_{1}$ переходит в прямую $BD$ пусть $H' \in OH \cap w_{1}, \ E' \in OE \cap X, \ G' \in OG \cap Y$ тогда получается $H', \ E', \ G'$ соответственно образы $H, \ E, \ G$

Так как $OH \cdot OH' = OG \cdot OG' = OE' \cdot OE = OF' \cdot OF = OC^2$ откуда $GG'HH'C, \ FF'GG', \ EE'HH'A$ вписанные тогда $\angle F'G'H = \angle F'G'O+\angle HG'O = \angle F'FG + \angle GH'H = \angle F'FG + \angle GCH = 90^{\circ}$ из вписанности $EE'HH'A$ тогда $\angle F'E'H = \angle F'E'E+\angle EE'H = \angle CAO + \angle EAC = 90^{\circ}$ то есть $F'G'HE'$ вписанный в $w_{3}$ с диаметром $F'H$ и так как $BD \perp F'H$ из условия, тогда $BD$ касательная к $w_{3}$ а так как $w_{3}$ образ окружности $w_{2}$ относительно $w$ а $BD$ образ $w_{1}$ тогда и прообразы $w_{1}, \ w_{2}$ касаются

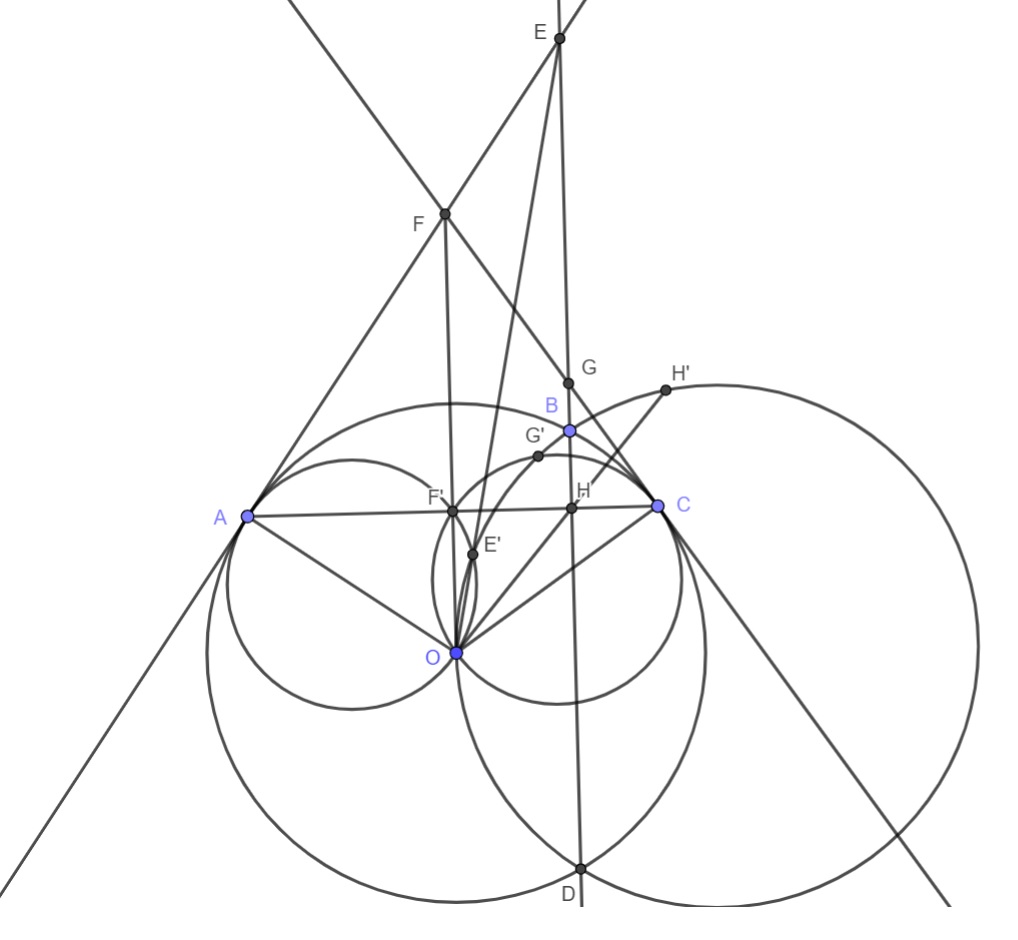
Пусть $X$ - точка пересечения касательных к окружности, $M$ - середина $AC$, $S=AC\cap BD$, $\omega$ - описанная окружность $\Delta$, $NX$ её диаметр, $H=BD\cap NX$. Несложно проверить, что при инверсии относительно $(ABCD)$ $X$ переходит $M$, следовательно $\Omega$(образ $\omega$) касается $OM$ в точке $M$. Требуется доказать, что $\omega$ касается $(BOD)\Leftrightarrow \Omega$ касается $BD$. Пусть $\Omega'$ касается $BD$ и $OM$ в точке $M$. Тогда докажем, что $\Omega=\Omega'\Leftrightarrow\Omega'$ гомотетичен $\omega$ относительно $O$$\Leftrightarrow N,S,O$ коллинеарны$\Leftrightarrow \frac{MS}{XN}=\frac{OM}{OX}$. Обозначим $\alpha=\angle AOM$. В окружности $\omega$ и четырёхугольнике $AXCO$, соответственно, легко посчитать $MS=XH=XN\sin^2\alpha$ и $OM=OX\sin^2\alpha$ - что требовалось доказать.