2-я международная Иранская олимпиада по геометрии, 2015 год, третья лига, 11-12 классы

В окружность $\omega$ с центром $O$ вписан правильный треугольник $ABC$. Пусть $P$ — точка дуги $BC$. Касательная прямая к $\omega$ в точке $P$ пересекает продолжения прямых $AB$ и $AC$ в точках $K$ и $L$ соответственно. Докажите, что $\angle{KOL} > 90^\circ$.

Комментарий/решение

1)Факт: косинус острого угла больше $0$. Напротив, если угол тупой, его косинус меньше $0$.

2)Рассмотрим скалярное произведение векторов $\overrightarrow{OK}$ и $\overrightarrow{OL}$

$$\overrightarrow{OK}\cdot \overrightarrow{OL} = \left| \overrightarrow{OK}\right|\cdot \left| \overrightarrow{OL}\right|\cdot \cos\angle{KOL}$$

Длины отрезков неотрицательны, а значит, скалярное произведение и косинус угла имеют одинаковый знак. То есть, если покажем, что $\overrightarrow{OK}\cdot \overrightarrow{OL}<0$, то из этого сразу же следует $ \cos\angle{KOL}<0$, а из этого - то, что $\angle{KOL}>90^\circ$

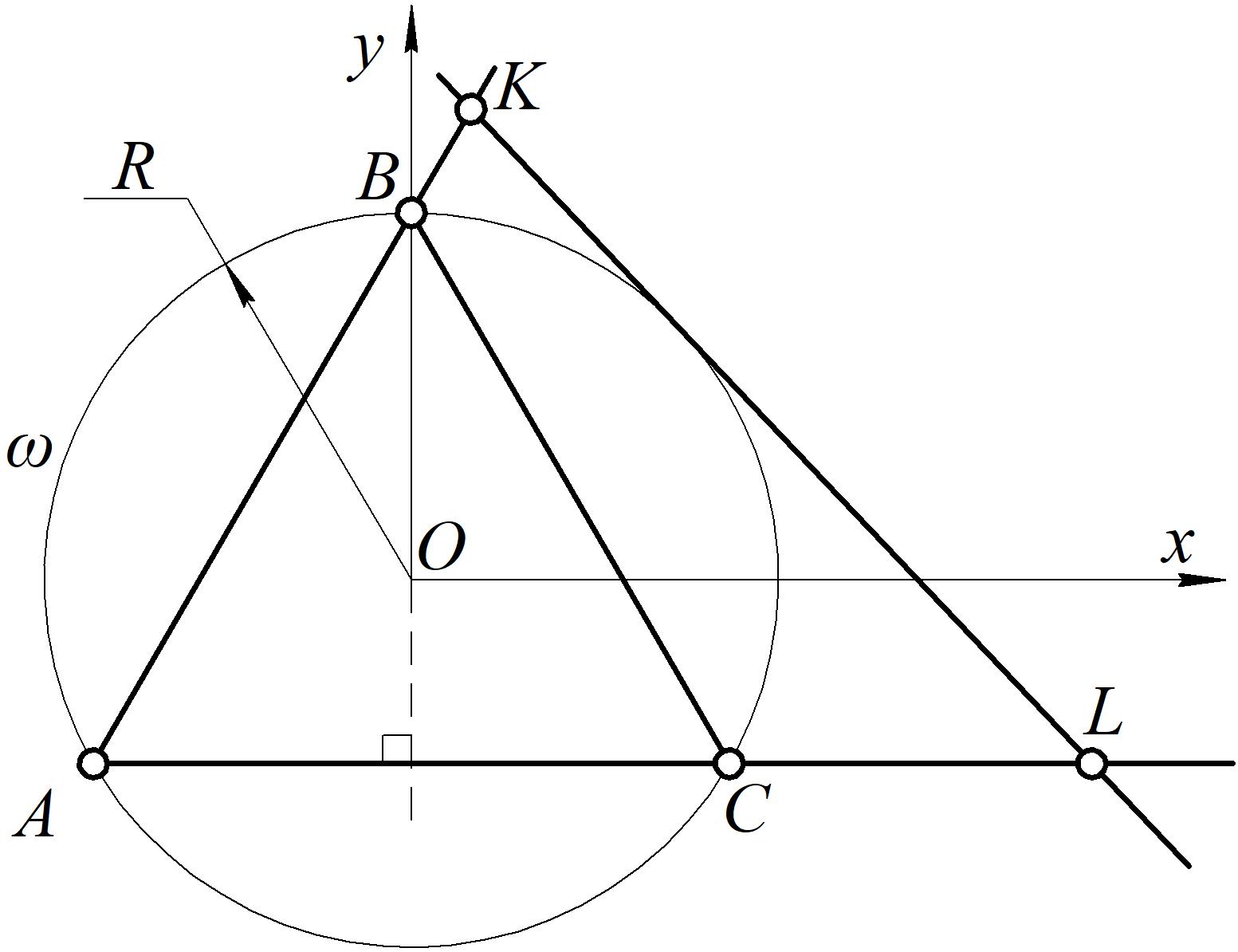
3)Введем систему координат как на рисунке. Тогда координаты будут:

$$A(-R\cdot\cos 30^\circ;-R\cdot\sin 30^\circ);\;\;\;B(0;R);\;\;\;C(R\cdot\cos 30^\circ;-R\cdot\sin 30^\circ);$$

$$O(0;0);\;\;\;P(R\cdot\cos\varphi;R\cdot\sin\varphi)$$

Угол $\varphi$ - это наклон отрезка $OP$ к оси $x$

4)Нормаль к прямой $KL$ - это вектор $\overrightarrow{OP}$, потому что касательная и радиус в точке касания перпендикулярны (да, я капитан очевидности)

Отсюда уравнение прямой $KL$

$$R\cdot\cos\varphi\cdot x+R\cdot\sin\varphi\cdot y + C_{kl} = 0$$

5)Подстановкой точки $P$ в прямую $KL$ выясняем значение $C_{kl}$

$$R\cdot\cos\varphi\cdot R\cdot\cos\varphi+R\cdot\sin\varphi\cdot R\cdot\sin\varphi + C_{kl} = 0 \rightarrow C_{kl}=-R^2$$

Окончательно получим уравнение прямой $KL$

$$KL:\;\;\;\;R\cdot\cos\varphi\cdot x+R\cdot\sin\varphi\cdot y -R^2 = 0$$

6) Уравнение прямой $AC$ получим вообще просто - так как $AC\parallel x$, и $Y_C=-R\sin 30^\circ$, то уравнение прямой $AC$ имеет вид:

$$AC:\;\;\;\;y+R\sin 30^\circ=0$$

7)Уравнение $AB$ тоже получим по-простому, без нормалей. Ведь известен наклон прямой $AB$ к оси $x$ - это $60^\circ$

$$AB:\;\;\;\;y=\tan 60^\circ\cdot x + y(0) = \sqrt 3\cdot x + R$$

8)$K=AK\cap KL\Rightarrow$

$$\begin{equation*} \begin{cases} y= \sqrt 3\cdot x + R \\ \cos\varphi\cdot x+\sin\varphi\cdot y -R=0 \end{cases}\end{equation*}$$

Надеюсь мне простят, если я сразу выдам решение этой системы

$$\boxed{K\left(\dfrac{R(1-\sin\varphi)}{\cos\varphi+\sqrt{3}\sin\varphi} ;\dfrac{R(\sqrt{3}+\cos\varphi)}{\cos\varphi+\sqrt{3}\sin\varphi}\right)}$$

9)$L=AC\cap KL\Rightarrow$

$$\begin{equation*} \begin{cases} y= -R/2 \\ \cos\varphi\cdot x+\sin\varphi\cdot y -R=0 \end{cases}\end{equation*}$$

Решение системы

$$\boxed{L\left(\dfrac{R(1+0.5\cdot\sin\varphi)}{\cos\varphi} ;\dfrac{R}{2}\right)}$$

10)Считаем $\overrightarrow{OK}\cdot \overrightarrow{OL}$

$$\overrightarrow{OK}\cdot \overrightarrow{OL} = X_k\cdot X_l + Y_k\cdot Y_l$$

$$\overrightarrow{OK}\cdot \overrightarrow{OL}=\dfrac{R(1-\sin\varphi)}{\cos\varphi+\sqrt{3}\sin\varphi}\cdot \dfrac{R(1+0.5\cdot\sin\varphi)}{\cos\varphi} + \dfrac{R(\sqrt{3}+\cos\varphi)}{\cos\varphi+\sqrt{3}\sin\varphi}\cdot\dfrac{R}{2} $$

Данное выражение строго меньше 0 при $-30^\circ<\varphi<90^\circ$