2-я международная Иранская олимпиада по геометрии, 2015 год, первая лига, 7-8 классы

На сторонах $AB$, $BC$, $CD$ и $AD$, прямоугольника $ABCD$, взяты точки $M$, $N$, $P$ и $Q$ соответственно так, что площади треугольников $AQM$, $BMN$, $CNP$, $DPQ$ равны. Докажите, что $MNPQ$ параллелограмм.

Комментарий/решение

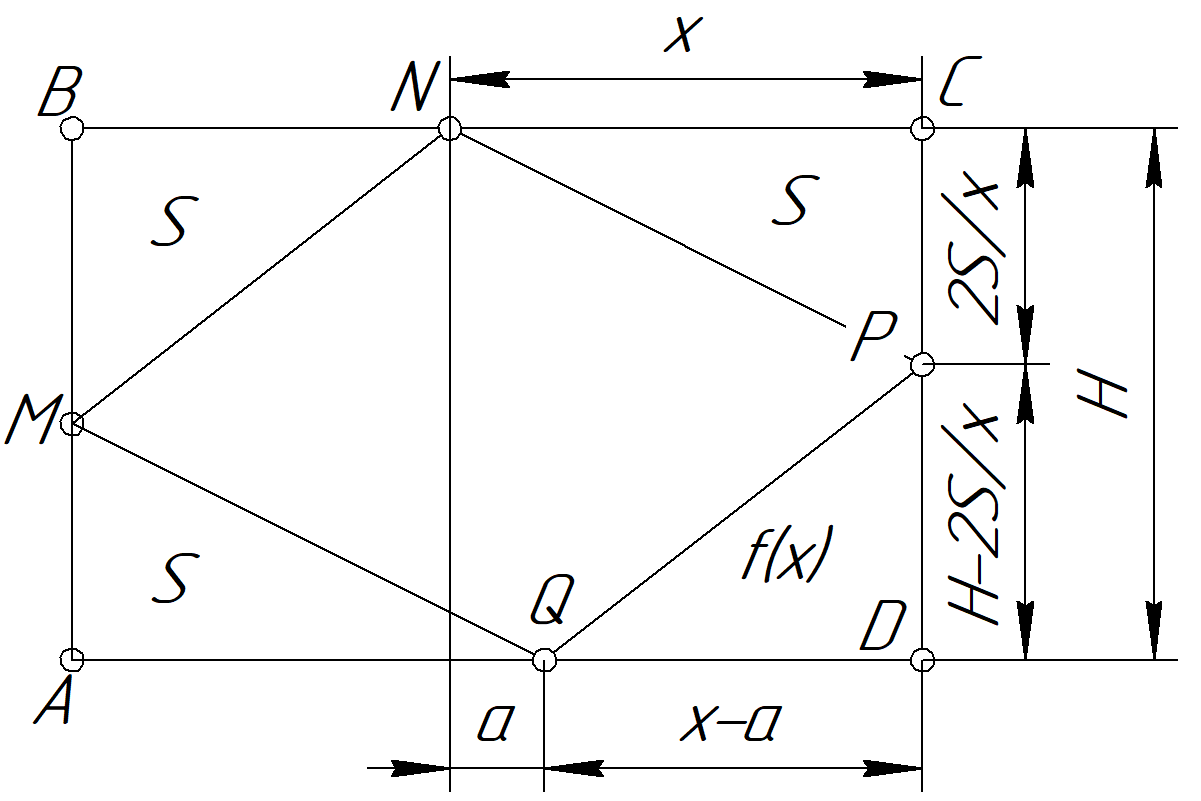
1) Пусть точки $Q,M$ проставлены произвольным образом. Обозначим $S_{\triangle AMQ}=S_{\triangle BMN}=S$.

2)Не уменьшая общности решения задачи, пусть $AQ>BN$

3)Теперь построим $\triangle NCP$. Пусть $NC=x$. Тогда, для выполнения условия (равенство площадей треугольников ), примем $S_{\triangle NCP}=S$

4)В таком случае $\dfrac{CP\cdot NC}{2}=S\Rightarrow CP=\dfrac{2S}{x}$

5) Пусть $CD=H$, отсюда $PD=H-\dfrac{2S}{x}$

6) Пусть $AQ-BN=a$, тогда $QD=x-a$

7) Обобщая пункты $[1-6]$, можно найти площадь $\triangle QPD$

$S_{\triangle QPD}=f(x)=\dfrac{(x-a)\cdot {(H-\dfrac{2S}{x})}}{2}=\dfrac{Hx-2S-aH+\dfrac{2Sa}{x}}{2}$

8) по условию, точка $P$ лежит на отрезке $CD$,отсюда $H-\dfrac{2S}{x}>0\Rightarrow H>\dfrac{2S}{x}$

9)Покажем, что при условии $[8]$ функция монотонно возрастает

$f'(x)=\dfrac{H-\dfrac{2Sa}{x^2}}{2}>\dfrac{\dfrac{2S}{x}-\dfrac{2Sa}{x^2}}{2}=\dfrac{2S}{2x}\cdot{(1-\dfrac{a}{x})}>0$

Ведь $S,x-$положительные, $a<x\Rightarrow \dfrac{a}{x}<1$

Производная положительная для любого $x$, удовлетворяющего условию $[8]$

То есть монотонно возрастает

Отсюда ясно, что у уравнения $f(x)=S$ единственное решение

9) и этим решением будет равенства $\triangle AMQ=\triangle CNP;\triangle MBN=\triangle QDP$. Не сложно проверить, что это удовлетворяет условию: ведь площади всех этих треугольников равна $S$

10) Из $[9]$ следует $MQ=NP;MN=QP$

Из равенства противоположных сторон следует, что $MNPQ-$параллелограмм

Пусть $AB=x, \ BC=y, \ BN=a, NC=y-a, \ BM=b, \ AM=x-b, \ AQ=c, \ QC=y-c, \ DP=d, \ CP=x-d$

По условию $S=S_{AQM}=S_{BMN}=S_{CNP}=S{DPQ}$ или $ab=(x-b)c=(y-c)d=(x-d)(y-a)$

Откуда $c = \dfrac{ab}{x-b}$ подставляя в третье решая с первым $d = \dfrac{ab}{y-\dfrac{ab}{x-b}}$ решая последнее с первым

$ab = (x - \dfrac{ab}{y-\dfrac{ab}{x-b}}) (y-a)$

Откуда $\dfrac{ (2ab-xy)(ax+by-xy)}{ab+by-xy}=0$

1) $ab=\dfrac{xy}{2}$ так как $4S<S_{ABCD}$ но $4S=2xy=2S_{ABCD}$ что не верно

2) $b=x-\dfrac{ax}{y}$ тогда $d=b=x-\dfrac{ax}{y}$ и $c=y-a$ откуда получаем по равенству отрезков $MNPQ$ параллелограмм.

Возмем AB и CD как X , AD и BC как Y тогда MB=X-a BN=Y-b QD=Y-z DP=X-d.

Если a>d тогда X-d>X-a и za=db z<b и значит Y-b>Y-z с этого

(X-d)(Y-z)>(X-a)(Y-b) значит площади треугольника DPQ>BNM а это не возможно значит X=Y по равенству прямоугольные треугольники по парно равны значит MNPQ параллелограмм