Математикадан аудандық олимпиада, 2015-2016 оқу жылы, 10 сынып

Қабырғасы 1-ге тең $ABCD$ шаршысына сырттай сызылған шеңбердің $BC$ доғасынан $M$ нүктесі алынған. $AM$ және $BD$ кесінділері $P$ нүктесінде, ал $DM$ және $AC$ кесінділері — $Q$ нүктесінде қиылысады. $APQD$ төртбұрышының ауданын табыңыз.

Комментарий/решение

Комментарии от администратора Комментарии от администратора №1.     Ответ. $0,\!5$.
Решение. Пусть отрезки $AM$ и $BC$ пересекаются в точке $N$, а отрезки $PQ$ и $ND$ — в точке $K$. Угол $AMD$ опирается на дугу $AD$, поэтому он равен $45^\circ$. А так как и $\angle QCN = 45^\circ$, то точки $N$, $M$, $C$, $Q$ лежат на одной окружности. Следовательно $\angle MDB = \angle MCB = \angle MQN$, то есть $NQ allel BD$ или $PNQD$ — трапеция. У треугольников $PND$ и $PQD$ есть общее основание, поэтому их площади равны. А так как в этих площадях есть также общая площадь треугольника $PKD$, то $S_{PNK}=S_{KDQ}$. Итак имеем: $$S_{APQD}=S_{APKD}+S_{KDQ}=S_{APKD}+S_{PNK}=S_{AND}=0,\!5.$$

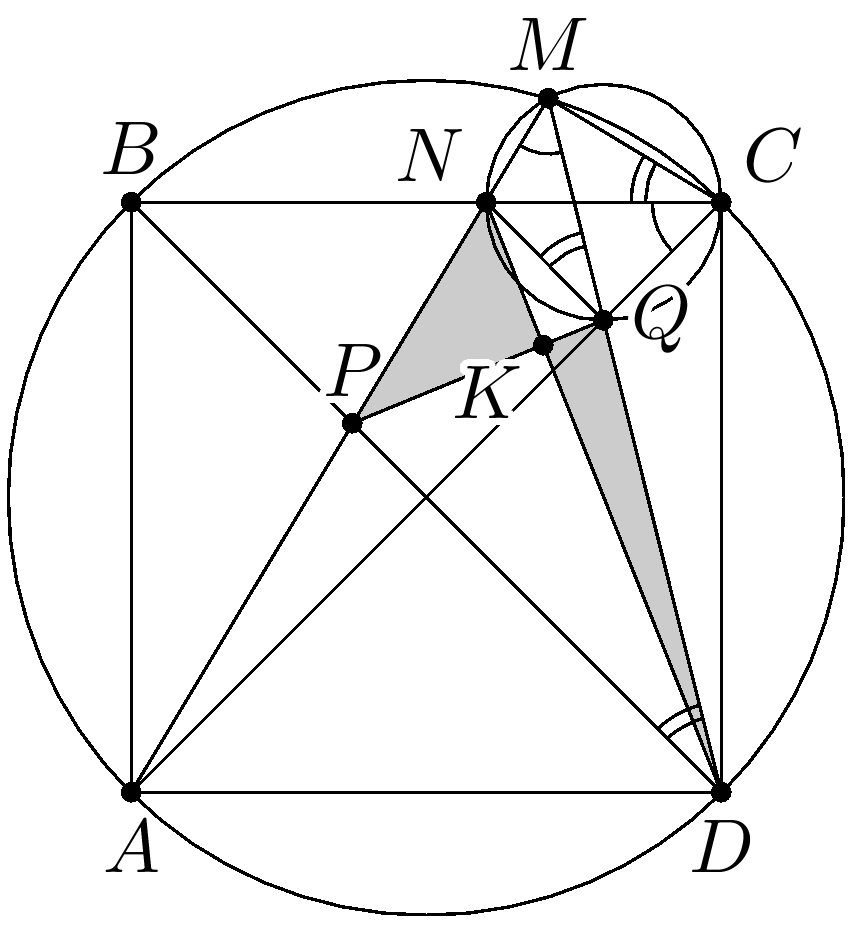
шешуі: $М$ нүктесі ВС доғасының ортасы болсын делік. Онда $доғаВМ = доғаСМ$, $\angle ВДМ = \angle СДМ$, яғни $ДМ$ $ВДС$ бұрышының биссектрисасы болады.

$\triangle ДОС$-дан $\frac{OD}{OQ} = \frac{CD}{CQ}$, $OQ= OC - CQ$ болғандықтан $\frac{R}{R-CQ} = \frac{1}{CQ} \implies CQ = \frac{R}{R+1}$.

Ал, $OQ = R - \frac{R}{R+1} = \frac{R^2}{R+1}$, $R = \frac{\sqrt{2}}{2}$, яғни $OQ = \frac{1}{\sqrt{2} + 2}$.

$OP = OQ$

$S_{\triangle APQD} = S_{\triangle POQ} + 2S_{\triangle POA} + S_{\triangle AOD}$

$S_{\triangle POQ} = \frac{OP \cdot OQ}{2} = \frac{1}{2(\sqrt{2}+2)^2}$,

$2S_{\triangle POA} = 2 \cdot \left(\frac{1}{\sqrt{2} + 2} \cdot \frac{\sqrt{2}}{2}\right)/2 = \frac{\sqrt{2}}{2(\sqrt{2}+2)}$,

$S_{\triangle AOD} = \frac{\sqrt{2}/2 \cdot \sqrt{2}/2}{2} = \frac{1}{4}$.

$S_{\triangle APQD} = \frac{1}{2(\sqrt{2}+2)^2} + \frac{\sqrt{2}}{2(\sqrt{2}+2)} + \frac{1}{4} = \frac{2\sqrt{2}+3}{(\sqrt{2}+2)^2} = \frac{1}{2}$.

Жауап: $\frac{1}{2}$