Қалалық Жәутіков олимпиадасы 8 сынып, 2013 жыл

Дөңес $ABCD$ төртбұрышында мына қатынастар орындалады: $\angle DAB=\angle ABC=60{}^\circ $ және $\angle CAB=\angle CBD$. $AD+CB=AB$ болатынын дәлелдеңдер.

Комментарий/решение

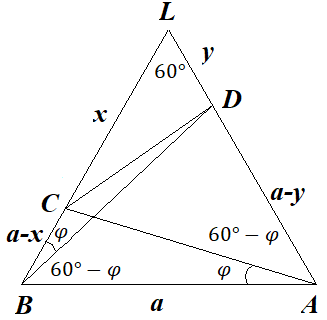
1)Пусть $BC \cap AD = L$

2)Теорема : треугольник со всеми равными углами является равносторонним

3) $\Delta ABL-$ равносторонний, так как $\angle ABC = 60^\circ;\angle DAB = 60^\circ;$

$$\angle BLA = 180^\circ - (\angle ABC + \angle DAB) = 180^\circ - 60^\circ - 60^\circ = 60^\circ$$

4) Тогда примем $AB = BL = AL = a$

5) Пусть $LC = x; LD = y;$ Тогда $BC = BL- CL = a-x; AD = AL - DL = a - y$

6) По условию $\angle CBD = \angle CAB = \varphi$

7) Рассмотрим $\Delta BDL$. По теореме синусов

$$\dfrac{DL}{\sin\angle DBL}=\dfrac{BL}{\sin\angle BDL}$$

$$\angle DBL = \varphi;\angle BDL = 180^\circ - (60^\circ + \varphi)=120^\circ - \varphi$$

Откуда имеем

$$\dfrac{y}{\sin\varphi}=\dfrac{a}{\sin(120^\circ-\varphi)}\Rightarrow y=a\cdot\dfrac{\sin\varphi}{\sin(120^\circ-\varphi)}$$

8) Рассмотрим $\Delta ABC$. По теореме синусов

$$\dfrac{BC}{\sin\angle CAB}=\dfrac{AB}{\sin\angle BCA}$$

$$\angle CAB = \varphi;\angle BCA = 180^\circ - (60^\circ + \varphi)=120^\circ - \varphi$$

Откуда имеем

$$\dfrac{a-x}{\sin\varphi}=\dfrac{a}{\sin(120^\circ-\varphi)}\Rightarrow x=a-a\cdot\dfrac{\sin\varphi}{\sin(120^\circ-\varphi)}$$

9) $BC+AD = a-x+a-y = 2a-(x+y);$

$$x+y = a-a\cdot\dfrac{\sin\varphi}{\sin(120^\circ-\varphi)}+a\cdot\dfrac{\sin\varphi}{\sin(120^\circ-\varphi)}=a\forall \varphi$$

Из выражения выше следует что

$$BC+AD = a = AB$$

Доказательство завершено

$L \in BC \cap AD$ то есть $AB=BL=AL$ , возьмем на $BL$ такую точку $C'$ что $BC' = AD$ тогда из условия Если $\angle DAC = x$ тогда $ \angle BC'A = \angle BDA = 120-x$ то есть $\angle AC'C = 60+x$ но с другой стороны $\angle BCA = 180-60-(60-x) = 60+x$ то есть $AC' = AC$ тогда $CL = BC' = AD$ то есть $BC+AD = BC+BC' = BC+CL = BL = AB$.