Городская Жаутыковская олимпиада, 8 класс, 2012 год

На стороне $AD$ параллелограмма $ABCD$ взята точка $R$, а на сторонах $AB$ и $CD$ точка $P$ и $Q$ соответственно так, что отрезки $PR$ и $QR$ параллельны диагоналям параллелограмма. Докажите, что площади треугольников $PBR$ и $QCR$ равны.

Комментарий/решение

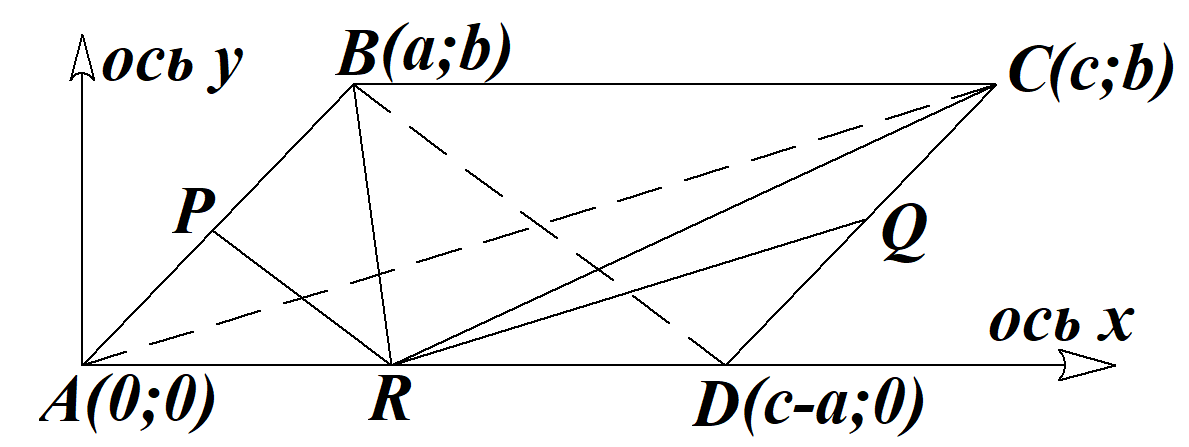
1) Введём систему координат: $Ax\parallel AD;Ay\bot AD$. В этой системе координат $A(0;0);B(a;b);C(c;b);D(c-a;0)$

2) По условию, $PR\parallel BD;RQ\parallel AC$. Поэтому, $\angle APR=\angle ABD$ (как односторонние при параллельных прямых). Аналогично $\angle DRQ=\angle DAC$.

3) Из $(2)$ следует подобие треугольников: $$\triangle APR\sim\triangle ABD;\triangle DRQ\sim\triangle DAC$$

4) Из подобия треугольников (см.$(3)$) имеем

$$\dfrac{DA}{RA}=\dfrac{BA}{PA}$$

5) Домножим числитель и знаменатель выражения $(4)$ вначале на $\cos\angle BAD$, а затем на $\sin\angle BAD$.

$$\dfrac{BA}{PA}=\dfrac{BA\cdot\cos\angle BAD}{PA\cdot\cos\angle BAD}=\dfrac{X_B}{X_P}$$

$$\dfrac{BA}{PA}=\dfrac{BA\cdot\sin\angle BAD}{PA\cdot\sin\angle BAD}=\dfrac{Y_B}{Y_P}$$

Аналогично

$$\dfrac{AD}{RD}=\dfrac{CQ}{DQ}=\dfrac{X_C}{X_Q}=\dfrac{Y_C}{Y_Q}$$

6) Используем выражения $(4,5)$ для нахождения координат точек $P$ и $Q$

$$\dfrac{c-a}{d}=\dfrac{X_B}{X_P}=\dfrac{a}{X_P}\rightarrow X_P=\dfrac{a\cdot d}{c-a}$$

$$\dfrac{Y_B}{Y_P}=\dfrac{X_B}{X_P}\rightarrow Y_P=\dfrac{Y_B\cdot X_P}{X_B}=\dfrac{b\cdot\dfrac{a\cdot d}{c-a}}{a}=\dfrac{b\cdot d}{c-a}$$

Координаты точки $P$ найдены.

$$\dfrac{c-a}{c-a-d}=\dfrac{X_C}{X_Q}=\dfrac{c}{X_Q}\rightarrow X_Q=\dfrac{c(c-a-d)}{c-a}$$

$$\dfrac{Y_C}{Y_Q}=\dfrac{X_C}{X_Q}\rightarrow Y_Q=X_Q\cdot\dfrac{Y_C}{X_C}=\dfrac{c(c-a-d)}{c-a}\cdot\dfrac{b}{c}=\dfrac{b\cdot (c-a-d)}{c-a}$$

Координаты точки $Q$ найдены.

7) Площадь треугольника $S_{\triangle PBR}$ может быть посчитана при помощи векторного произведения векторов

$$S_{\triangle PBR}=\dfrac{1}{2}\cdot |\overrightarrow{RP}\times \overrightarrow{RB}|$$

Аналогично рассчитаем площадь $S_{\triangle CRQ}$

$$S_{\triangle CRQ}=\dfrac{1}{2}\cdot |\overrightarrow{RC}\times \overrightarrow{RQ}|$$

8) Известны все нужные координаты, осталось найти вектора.

$$\overrightarrow{RP}=(\dfrac{a\cdot d}{c-a}-d; \dfrac{b\cdot d}{c-a})=(\dfrac{2ad-dc}{c-a};\dfrac{b\cdot d}{c-a})$$

$$\overrightarrow{RB}=(a-d;b)$$

$$\overrightarrow{RC}=(c-d;b)$$

$$\overrightarrow{RQ}=(\dfrac{c}{c-a}\cdot (c-a-d);\dfrac{b}{c-a}\cdot (c-a-d))$$

9) Рассчитаем векторные произведения

$$S_{\triangle RPB}=\dfrac{1}{2}\cdot \begin{vmatrix}\overrightarrow i & \overrightarrow j & \overrightarrow k\\\dfrac{2ad-dc}{c-a} & \dfrac{bd}{c-a} & 0\\a-d & b & 0\end{vmatrix}$$

$$S_{\triangle RPB}=\dfrac{1}{2\cdot (c-a)}\cdot |\overrightarrow k\cdot (b\cdot (2ad-dc)-bd\cdot(a-d))|=\dfrac{bda-bdc+bd^2}{2(c-a)}$$

$$S_{\triangle RPB}=\dfrac{bd}{2\cdot (c-a)}\cdot(a-c+d)$$

10) Расчёт векторного произведения

$$S_{\triangle RCQ}=\dfrac{1}{2}\cdot \begin{vmatrix}\overrightarrow i & \overrightarrow j & \overrightarrow k\\c-d & b & 0\\ \dfrac{c(c-a-d)}{2(c-a)} & \dfrac{b(c-a-d)}{2(c-a)} & 0\end{vmatrix}$$

$$S_{\triangle RCQ}=\dfrac{c-a-d}{2\cdot (c-a)}\cdot (b\cdot (c-d)-bc)$$

$$S_{\triangle RCQ}=\dfrac{bd}{2\cdot (c-a)}\cdot(a-c+d)$$

11) Очевидно из $(9,10)$, что искомые площади равны.

По теореме Фалеса для треугольников $DRQ, DAC$ получается $\dfrac{CQ}{DQ} = \dfrac{AR}{DR}$ так же и для $\dfrac{AP}{BP} = \dfrac{AR}{DR}$ откуда $\dfrac{AP}{BP} = \dfrac{CQ}{DQ}$ или $\dfrac{AB}{BP} = \dfrac{AB}{DQ}$ откуда $BP=DQ$

Проведем высоты $RE,RF$ из вершины $R$ на соответственные стороны $AB,CD$ из подобия треугольников $REA,RDF$ получается $\dfrac{RE}{RF} = \dfrac{AR}{DR}$ но $\dfrac{BP}{CQ} = \dfrac{AR}{DR} = \dfrac{RE}{RF}$ или $RF \cdot BP = RE \cdot CQ$ значит $S_{PBR} = S_{QCR}$