Городская Жаутыковская олимпиада, 9 класс, 2008 год

Биссектриса треугольника делит одну из его сторон на отрезки 3 см и 5 см. В каких границах меняется периметр треугольника?

Комментарий/решение

Ответ : $P_{\Delta ABC}\in (16;40)$

Решение

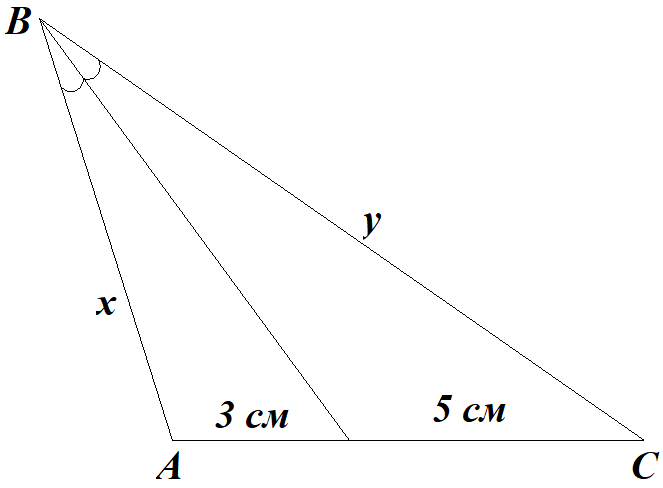
1) Теорема: Биссектриса угла треугольника делит противоположную сторону на части, пропорциональные прилежащим сторонам треугольника.

2) Из теоремы (1) имеем

$$\dfrac{x}{3}=\dfrac{y}{5}$$

3) Неравенства треугольника:

$$x+y>8\;\;\;\;;x+8>y\;\;\;\;;y+8>x$$

4) Пусть $x = 3+\varepsilon$, тогда $y=\dfrac{5\cdot (3+\varepsilon)}{3}=5+\dfrac{\varepsilon}{3}$

Устремляя эпсилон к нулю , рассчитаем периметр

$$\mathop {\lim } \limits_{ \varepsilon \to 0}P_{\Delta ABC} = 3+\varepsilon +5+\dfrac{\varepsilon}{3} + 8 = 16 + \dfrac{4}{3}\cdot\varepsilon=16$$

Понятно, что предельный случай не может быть реализован, так как вершина $B$ будет лежать на стороне $AC$. То есть, $16$ - минимум периметра рассматриваемого треугольника

5) Максимума периметра можно достигнуть, если устремить $x+8\rightarrow y$

$$x+8=y\rightarrow x+8=\dfrac{5x}{3}\rightarrow \dfrac{2}{3}\cdot x = 8\rightarrow x = 12$$

Откуда $y=\dfrac{5}{3}\cdot 12 = 20$

Периметр равен $P_{\Delta ABC}=12+20+8=40$

Этот предельный случай тоже не реализуем, ведь тогда $A,B,C$ лягут на одну прямую