Қалалық Жәутіков олимпиадасы 9 сынып, 2001 жыл
Комментарий/решение:
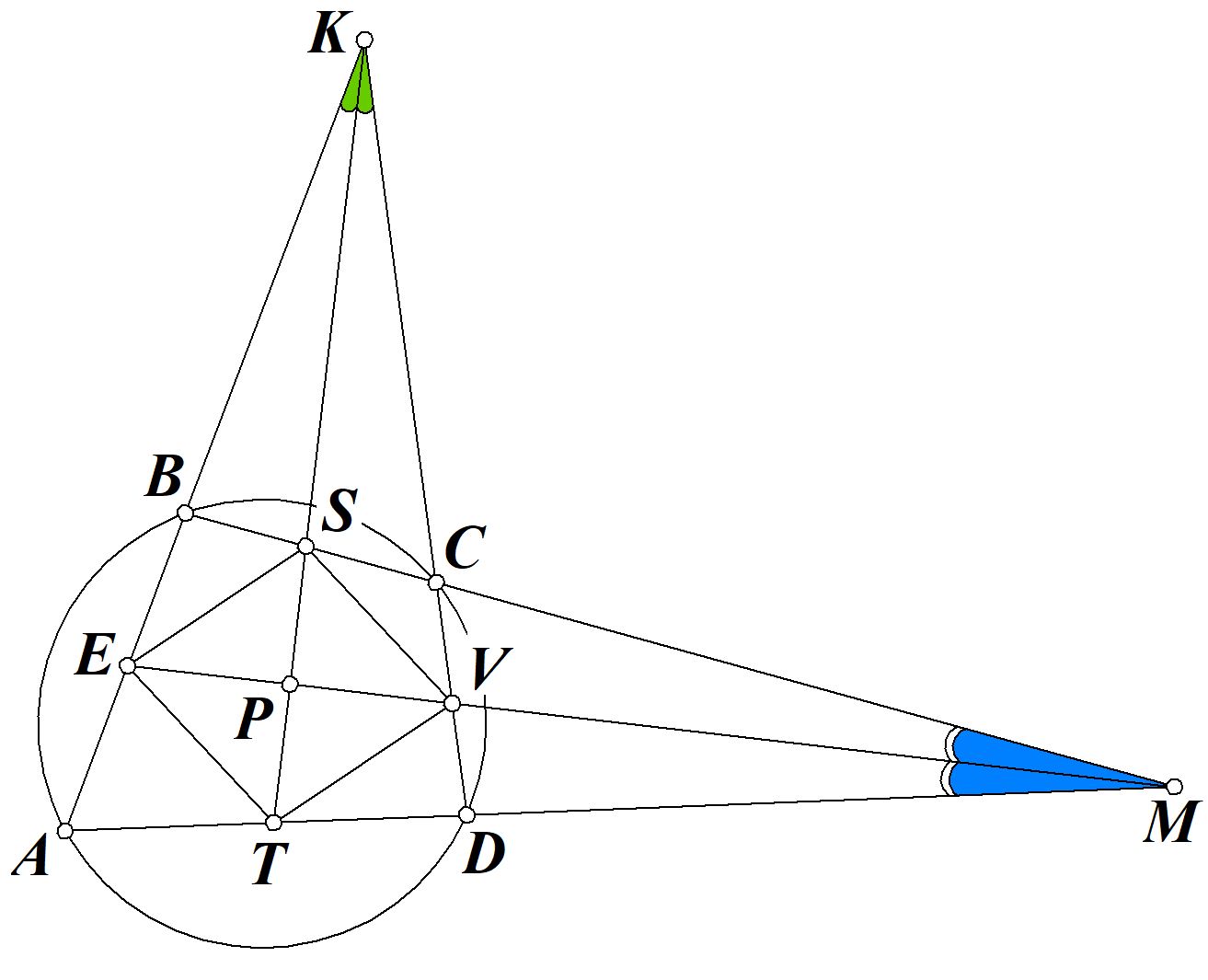
1)Теорема: Сумма противоположных углов вписанного четырёхугольника равна $180^\circ$
2)Теорема: У ромба диагонали пересекаются под прямым углом
3)Теорема: У ромба диагонали пересекают друг друга пополам.
4)Пусть $\angle AKT=\angle DKT=\alpha$ ($KT-$ биссектриса по условию).
Также пусть $\angle BME=\angle AME=\beta$ ($ME-$ биссектриса по условию).
5)Обозначим угол $\angle BAD=\varphi$
6) Так как $ABCD-$ вписанный в окружность, по теореме $(1)$ имеем $$\angle BAD+\angle BCD=180^\circ\rightarrow \angle BCD=180^\circ-\varphi$$
7)Углы $\angle BCD$ и $\angle BCK-$ смежные, а значит их сумма $180^\circ$
$$\angle BCD+\angle BCK=180^\circ\rightarrow \angle BCK=180^\circ-(180^\circ-\varphi)=\varphi$$
8)Рассмотрим $\triangle KSC$. Найдём в нём угол $\angle KSC$
$$\angle KSC+\angle SCK+\angle SKC=180^\circ\rightarrow \angle KSC+\angle BCK+\angle DKT=180^\circ$$
$$\angle KSC=180^\circ-\alpha-\varphi$$
9) Углы $\angle PSC$ и $\angle KSC-$ смежные, а значит их сумма $180^\circ$
$$\angle PSC +\angle KSC =180^\circ\rightarrow \angle BCK=180^\circ-(180^\circ-\alpha-\beta)=\alpha+\varphi $$
10)$\angle PSC=\angle BSK=\alpha+\varphi$ (как вертикальные)
11) Рассмотрим $\triangle BSK$. Найдём в нём угол $\angle KBS$
$$\angle BSK+\angle BKS+\angle KBS=180^\circ\rightarrow \angle BSK+\angle AKT+\angle KBS=180^\circ$$
$$\angle KBS=180^\circ-2\alpha-\varphi$$
12)Углы $\angle KBS$ и $\angle EBS-$ смежные, а значит их сумма $180^\circ$
$$\angle KBS +\angle EBS=180^\circ\rightarrow \angle EBS=180^\circ-(180^\circ-2\alpha-\varphi)=2\alpha+\varphi $$
13) Рассмотрим $\triangle BEM$. Найдём в нём угол $\angle BEM$
$$\angle BEM+\angle EBM+\angle BME=180^\circ\rightarrow\angle BEM+\angle EBS+\angle BME=180^\circ$$
$$\angle BEM=180^\circ-2\alpha-\varphi-\beta$$
14) Углы $\angle AEM$ и $\angle BEM-$ смежные, а значит их сумма $180^\circ$
$$\angle AEM+\angle BEM=180^\circ\rightarrow \angle AEM=180^\circ-(180^\circ-2\alpha-\varphi-\beta)=2\alpha+\varphi+\beta $$
15)Рассмотрим $\triangle AEM$. Просуммируем в нём углы.
$$\angle AEM+\angle AME+\angle EAM=180^\circ\rightarrow\angle BAD+\angle AEM+\angle AME=180^\circ$$
$$\varphi+(2\alpha+\varphi+\beta)+\beta=180^\circ\rightarrow\alpha+\beta+\varphi=90^\circ$$
16) Рассмотрим $\triangle PSM$. Просуммируем в нём углы.
$$\angle SPM+\angle PSC+\angle BME=180^\circ$$
$$\angle SPM+(\alpha+\varphi)+\beta=180^\circ\rightarrow\angle SPM=90^\circ$$
Здесь воспользовались фактом $(15)$
17) Рассмотрим $\triangle KEV$ и $\triangle MST$. В них $KP$ и $MP$ соответственно являются одновременно биссектрисами (по условию) и высотами (доказано в $(16)$) То есть, $\triangle KEV$ и $\triangle MST-$ равнобедренные, и $EP=PV;SP=PT$
18) Четырёхугольник $ESVT$ удовлетворяет теоремам $(2,3)$, значит, $ESVT-$ ромб
Легкое решение: $\angle PSC=\angle BSK=180-\angle BKS-\angle SBK=180-\angle BKS-\angle TDK=180-\angle TKD-\angle TDK=\angle STM, \Rightarrow SM=TM$, но $MP$ - биссектриса, $\Rightarrow SP=PT$ and $\angle SPV=90$, аналогично доказываем, что $EP=PV$, тогда $ESVT$ - ромб.
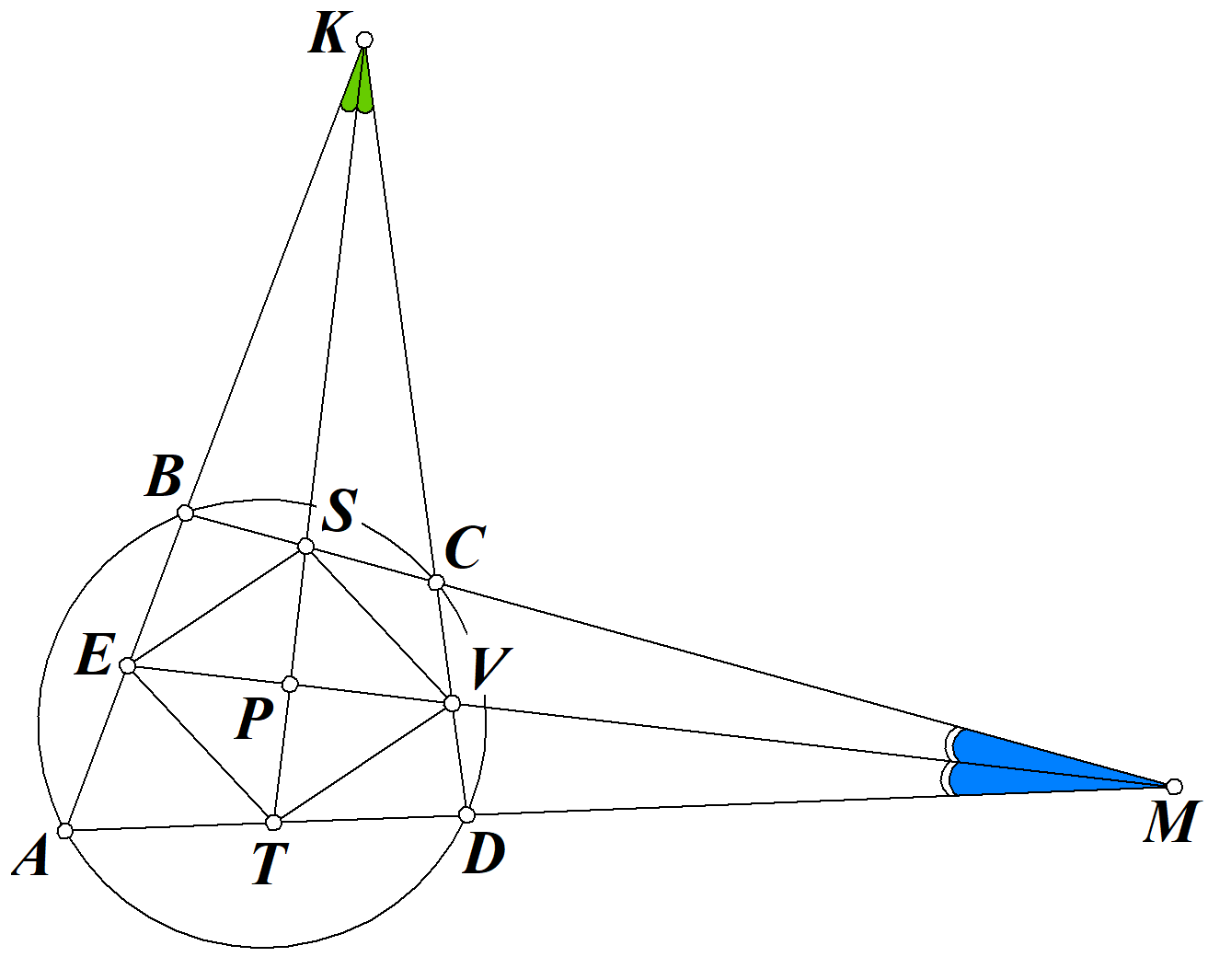
Возможно, что при неправильном наборе формул, они будут
доредактированы модератором. При этом содержание не будет меняться.