Олимпиада имени Леонарда Эйлера2014-2015 учебный год, II тур регионального этапа

На шахматной доске размером $20\times20$ расставлены 220 коней, которые бьют все свободные клетки. Докажите, что можно убрать 20 коней таким образом, чтобы оставшиеся кони били все свободные клетки. Напомним, что конь бьёт буквой «Г» (см. рисунок).

( С. Берлов )

Комментарий/решение

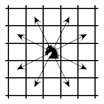
Комментарии от администратора Комментарии от администратора №1.     Решение. Будем убирать коней с доски по одному следующим образом. Если на очередном шаге можно убрать какого-то коня так, что оставшиеся будут бить все свободные поля, сделаем это. Если после некоторого шага останется 200 коней, мы получим требуемое. Предположим, что в некоторый момент ни одного коня с сохранением нужного условия убрать нельзя. Разобьём клетки доски на пары, соединённые ходом коня (это можно сделать, например, как на рисунке справа). Назовём пару полной, если в ней стоят два коня, и пустой, если в ней нет коней; пусть на доске $f$ полных и $e$ пустых пар. Рассмотрим любого коня $R$, стоящего в полной паре. Если его убрать, его клетка окажется побитой парным к нему; значит, останется непобитой некоторая другая клетка $C$. Ясно, что она находится в пустой паре и бьётся только конём $R$; сопоставим клетку $C$ коню $R$. Ясно, что разным коням сопоставлены разные клетки; поэтому общее количество сопоставленных клеток (оно не больше $2e$) равно $2f$, то есть $e \geq f$. Но общее количество коней равно $2f+(200-e-f) = 200+(f-e) \leq 200$. Значит, в момент, когда ни одного коня убрать нельзя, мы уже добились требуемого.