9-я Международная Жаутыковская олимпиада, 2013 год

Дана трапеция $ABCD$ ($AD\parallel BC$), в которой $\angle ABC > 90^\circ$. На боковой стороне $AB$ отмечена точка $M$. Обозначим через $O_1$ и $O_2$ центры описанных около треугольников $MAD$ и $MBC$ окружностей соответственно. Известно, что описанные около треугольников $MO_1D$ и $MO_2C$ окружности вторично пересекаются в точке $N$. Докажите, что прямая $O_1O_2$ проходит через точку $N$.

Комментарий/решение

Пусть $E$ точка пересечения $CD$ с окружность описанной около треугольника $AMD$, тогда $\angle MAD = \angle MED$ но так как $AD \ || \ BC$ то $\angle ABM = 180^{\circ}-MAD$ то есть $E$ лежит на окружности описанной около треугольника $MBC$ , получаем что $\angle MO_{1}D = \angle MO_{2}C$ и $\angle O_{2}MC = \angle O_{1}MD$. Пусть $F$ точка пересечения $CD$ с описанной окружностью около треугольника $MO_{2}C$, тогда $\angle O_{2}NC = \angle O_{2}MC$ , так как $O_{2}M=EO_{2}$ и $MO_{1}=EO_{1}$ как радиусы, то $O_{1}O_{2}$ биссектриса $\angle MO_{2}E$, откуда $\angle MO_{2}O_{1}+ \angle MO_{2}F = \angle MCE + \angle MCF = 180^{\circ}$ то есть $F$ лежит на прямой $O_{1}O_{2}$ и так как $\angle O_{1}MD = \angle O_{2}MC = \angle O_{2}FC$ получаем что $F=N$ откуда $N$ лежит на $O_{1}O_{2}$.

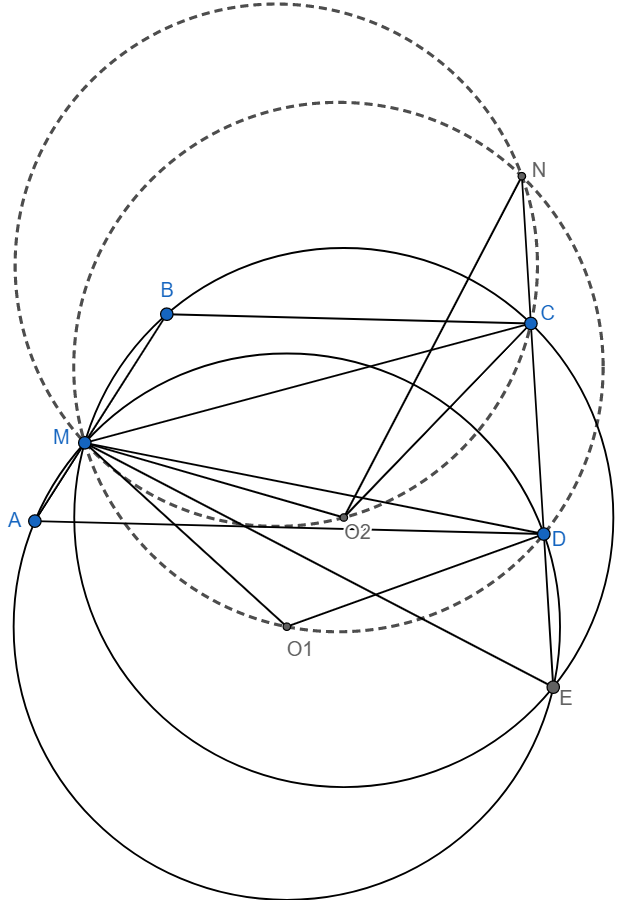
легко увидеть, что $M$ - центр поворотной гомотетии, переводящей $MO_1D$ в $MO_2C$. Тогда по третьему воробью получаем, что если пересечь $O_1O_2$ с $CD$ в $N'$, затем описать окружность около $N'O_2C$ и $N'O_1D$, они будут пересекаться в точке $M$, значит $N'=N$, причем $N$ лежит на $O_1O_2$