Решения: Олимпиада им. Леонарда Эйлера, Дистанционный этап

Олимпиада имени Леонарда Эйлера
2013-2014 учебный год, II тур дистанционного этапа

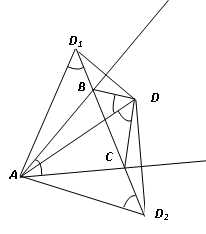
Внутри угла

$BAC$ , равного

$45^\circ$ , взята точка

$D$ так, что каждый из углов

$ADB$ и

$ADC$ равен

$45^\circ$ . Точки

$D_1$ и

$D_2$ симметричны точке

$D$ относительно прямых

$AB$ и

$AC$ соответственно. Докажите, что точки

$D_1$ ,

$D_2$ ,

$B$ и

$C$ лежат на одной прямой.

посмотреть в олимпиаде

Комментарий/решение:

Комментарии от администратора Комментарии от администратора №1. Решение. Так как треугольники $ABD$ и $ABD_1$ по условию симметричны, $AD_1 = AD$ , $\angle BAD_1 = \angle BAD$ , $\angle AD_1B = \angle ADB = 45^\circ$ .

Аналогично,

$AD_2 = AD$ ,

$\angle CAD_2 = \angle CAD$ ,

$\angle AD_2С = \angle ADС = 45^\circ$ . Из равенств

$\angle BAD_1 = \angle BAD$ , и

$\angle CAD_2 = \angle CAD$ следует, что

$\angle D_1AD_2 = 2 \angle BAC = 90^\circ$ . Так как при этом

$AD_1 = AD = AD_2$ , имеем

$\angle AD_1D_2 = \angle AD_2D_1 = 45^\circ$ . Таким образом,

$\angle AD_1D_2 = \angle AD_1B$ и

$\angle AD_2D_1 = \angle AD_2С$ , причем точки

$B$ и

$D_2$ лежат с одной стороны от прямой

$AD_1$ , а точки

$C$ и

$D_1$ — с одной стороны от прямой

$AD_2$ , откуда и следует утверждение задачи.

Олимпиада имени Леонарда Эйлера2013-2014 учебный год, II тур дистанционного этапа

Олимпиада имени Леонарда Эйлера
2013-2014 учебный год, II тур дистанционного этапа