Математикадан Эйлер олимпиадасы, 2013-2014 оқу жылы, Дистанциялық кезеңнің 2-ші туры


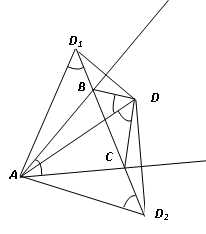
$45 ^\circ $-қа тең $BAC$ бұрышының ішінен $ADB$ мен $ADC$ бұрыштарының әрқайсысы $45 ^\circ $ болатындай $D$ нүктесі алынған. $D_1$ мен $D_2$ нүктелері сәйкесінше $AB$ мен $AC$ қарағанда $D$ нүктесіне симметриялы. $D_1$, $D_2$, $B$ және $C$ нүктелері бір түзудің бойында жататынын дәлелде.
посмотреть в олимпиаде

Комментарий/решение:

Комментарии от администратора Комментарии от администратора №1.     Решение. Так как треугольники $ABD$ и $ABD_1$ по условию симметричны, $AD_1 = AD$, $ \angle BAD_1 = \angle BAD$, $\angle AD_1B = \angle ADB = 45^\circ$.

Аналогично, $AD_2 = AD$, $ \angle CAD_2 = \angle CAD$, $\angle AD_2С = \angle ADС = 45^\circ$. Из равенств $\angle BAD_1 = \angle BAD$, и $ \angle CAD_2 = \angle CAD$ следует, что $\angle D_1AD_2 = 2 \angle BAC = 90^\circ$. Так как при этом $AD_1 = AD = AD_2$, имеем $\angle AD_1D_2 = \angle AD_2D_1 = 45^\circ$. Таким образом, $\angle AD_1D_2 = \angle AD_1B$ и $\angle AD_2D_1 = \angle AD_2С$, причем точки $B$ и $D_2$ лежат с одной стороны от прямой $AD_1$, а точки $C$ и $D_1$ — с одной стороны от прямой $AD_2$, откуда и следует утверждение задачи.