Математикадан Эйлер олимпиадасы, 2010-2011 оқу жылы, Дистанциялық кезеңнің 3-ші туры
Әрбір команда бір-бірімен бір рет қана ойнаған футбол жарысына $A$, $B$, $C$, $D$, $E$ және $F$ командалары қатысты. Жеңіс үшін командаға 3 ұпай, тең ойында 1 ұпай, ал жеңілген жағдайда 0 ұпай беріледі. Нәтижесінде $A$, $B$, $C$, $D$, $E$ командалары 7 ұпай алды. $F$ командасы ең үлкен қанша ұпай жинау мүмкін еді.
посмотреть в олимпиаде
Комментарий/решение:
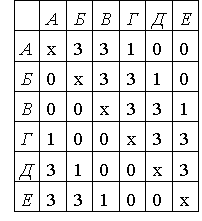
Комментарии от администратора Комментарии от администратора №1. Ответ. 7 очков. Решение. В матче, где одна из команд победила, команды вместе набирают 3 очка, в матче, закончившемся вничью — 2 очка. Поскольку 7 не делится на 3, команда, набравшая 7 очков, сделала хотя бы одну ничью. Так как таких команд пять, ничьих в турнире было сделано по крайней мере три. Всего матчей, как легко проверить, было сыграно 15. Поэтому все команды вместе набрали не больше, чем $2 \cdot 3+3 \cdot 12 = 42$ очка. Из них 35 очков набрали команды А, Б, В, Г и Д. Поэтому команда E набрала не больше $42-35 = 7$ очков. Как она могла набрать ровно 7 очков, показано в таблице внизу.
Возможно, что при неправильном наборе формул, они будут
доредактированы модератором. При этом содержание не будет меняться.