10-я Жаутыковская олимпиада (2014), теоретический тур
Задача №1. (10 баллов)
Эта задача состоит из трех частей, не связанных друг с другом. Задача 1А (3.0 балла)
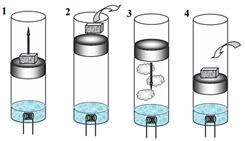
1. На поршне находится груз, включают нагреватель, вода кипит, пар поднимает поршень с грузом.
2. После того, как поршень поднялся на некоторую высоту, груз быстро снимают и вы-ключают нагреватель.
3. Пар под поршнем остывает и конденсируется, поршень медленно опускается.
4. После того как поршень опустился на определенную высоту, на него снова кладут груз. Постройте на диаграмме $(P,V)$ схематически цикл данной машины и найдите ее КПД. Атмосферное давление $P_0=10^5$ Па, масса поршня $M=2$ кг, его площадь $S=10$ см$^2$, масса груза $m=1$ кг. Ускорение свободного падения $g=9,8$ м/с$^2$. Считайте, что под поршнем находится только водяной пар. Зависимость давления насыщенного водяного пара от температуры в рассматриваемом диапазоне описывается функцией $P=at-b$, где, $a=4,85$ кПа/К, $b=384$ кПа, $t$ — температура в градусах Цельсия.
Задача 1В (5.0 балла)
Задача 1С (2.0 балла) Тонкая линза дает изображение предмета, расположенного перпендикулярно ее опти-ческой оси. Размер изображения $1$ см. Если расстояние от предмета до линзы увеличить на $5$ см, то опять получится изображение размером $1$ см. Каким будет размер изображения, если расстояние от предмета до линзы увеличить ещё на $5$ см?
комментарий/решение
Эта задача состоит из трех частей, не связанных друг с другом. Задача 1А (3.0 балла)
1. На поршне находится груз, включают нагреватель, вода кипит, пар поднимает поршень с грузом.
2. После того, как поршень поднялся на некоторую высоту, груз быстро снимают и вы-ключают нагреватель.
3. Пар под поршнем остывает и конденсируется, поршень медленно опускается.
4. После того как поршень опустился на определенную высоту, на него снова кладут груз. Постройте на диаграмме $(P,V)$ схематически цикл данной машины и найдите ее КПД. Атмосферное давление $P_0=10^5$ Па, масса поршня $M=2$ кг, его площадь $S=10$ см$^2$, масса груза $m=1$ кг. Ускорение свободного падения $g=9,8$ м/с$^2$. Считайте, что под поршнем находится только водяной пар. Зависимость давления насыщенного водяного пара от температуры в рассматриваемом диапазоне описывается функцией $P=at-b$, где, $a=4,85$ кПа/К, $b=384$ кПа, $t$ — температура в градусах Цельсия.
Задача 1В (5.0 балла)
Задача 1С (2.0 балла) Тонкая линза дает изображение предмета, расположенного перпендикулярно ее опти-ческой оси. Размер изображения $1$ см. Если расстояние от предмета до линзы увеличить на $5$ см, то опять получится изображение размером $1$ см. Каким будет размер изображения, если расстояние от предмета до линзы увеличить ещё на $5$ см?
комментарий/решение
Задача №2. Реактивное движение (10 баллов)
Классическая ракета Пусть ракета имеет начальную массу $m_0$, а скорость истечения топлива относительно ракеты постоянна и равна $u$. Считайте пока, что в начальный момент времени ракета покоится в лабораторной системе отсчета и внешние силы отсутствуют.
1. [0.5 балла] Найдите зависимость скорости ракеты $\vartheta$ от ее массы $m$. Эта формула называется формулой Циолковского. Ответ выразите через $m$, $m_0$, $u$.
2. [0.5 балла] Пусть объект массы $m=1000$ кг требуется разогнать до первой космической скорости. Найдите начальную массу ракеты $m_0$ с топливом, если $u=5$ км/с, ускорение свободного падения $g=9,8$ м/с$^2$, радиус Земли $R=6400$ км.
Пусть ракета движется в поле тяжести Земли, ускорение свободного падения $g$ которого будем считать постоянным, а расход топлива $\mu(t)=-dm(t)/dt$ может зависеть от времени.
3. [0.75 балла] Запишите уравнение движения ракеты в гравитационном поле Земли. Это уравнение называется уравнением Мещерского. Ответ выразите через $m$, $v$, $u$, $g$, $\mu$.
Далее считайте, что скорость истечения топлива $u$ направлена вдоль ускорения свободного падения $g$, а начальная скорость ракеты равна нулю.
4. [0.75 балла] Найдите, как расход топлива $\mu_{st}(t)$ должен зависеть от времени $t$, чтобы ракета висела на одной высоте неподвижно. Ответ выразите через $m_0$, $u$, $g$, $t$. Пусть теперь расход топлива постоянен во времени и равен $\mu$, причем всегда $\mu>\mu_{st}(t)$.
5. [2.0 балла] Тогда зависимость скорости ракеты $\vartheta(t)$ от времени $t$. может быть представлена в виде $$v(t)=A_1t+A_2ln(1+A_3t),$$ где $A_1$, $A_2$, $A_3$ — некоторые постоянные. Найдите $A_1$, $A_2$, $A_3$ и выразите их через $m_0$, $u$, $g$, $\mu$.
6. [1.0 балла] Пусть начальная масса ракеты равна $m_0$, а конечная масса — $m$. Найдите максимальную высоту $H_{\max}$, которую может достигнуть ракета и соответствующий расход топлива $\mu_{opt}$. Ответ выразите через $m_0$, $m$, $u$, $g$. Релятивистская ракета
В предыдущей части считалось, что ракета движется с нерелятивистской скоростью. Для осуществления межзвездных путешествий необходимо разгонять ракеты до скоростей, близких к скорости света и тогда в расчетах нельзя пренебрегать эффектами теории относительности. Для установления характера движения ракеты в релятивистском случае введем понятие сопутствующей системы отсчета. Сопутствующая система отсчета — это инерциальная система отсчета, которая движется относительно лабораторной системы отсчета со скоростью самой ракеты, то есть это система отсчета, в которой ракета в данный момент времени покоится.
7. [2.5 балла] Найдите связь ускорения ракеты в сопутствующей системе отсчета $a_{p}$ с ее ускорением в лабораторной системе отсчета $a_{r}$, если скорость ракеты в данный момент времени равна $v$, а скорость света — $c$. Ответ выразите через $a_{p}$, $a_{r}$, $v$, $c$.
8. [1.5 балла] Пусть ракета в начальный момент времени покоится. Тогда используя результаты предыдущего пункта можно показать, что масса ракеты в некоторый момент времени в сопутствующей системе отсчета связана с ее скоростью в лабораторной системе соотношением $$m=m_0\left(\frac{1-v/c}{1+v/c}\right)^{\alpha}.$$ Найдите $\alpha$ и выразите его через $u$, $c$.
9. [0.25 балла] Пусть объект массы $m=1000$ кг требуется разогнать до скорости $\vartheta=0,5$ с, равной половине скорости света $c=3\cdot 10^8$ м/с. Найдите начальную массу ракеты $m_0$ с топливом в виде степени с основанием $10$, если скорость истечения топлива $u=5$ км/с,
10. [0.25 балла] С точки зрения практики наилучшей является так называемая фотонная ракета, которая выбрасывает назад не раскаленные газы, получаемые при сгорании топлива, а фотоны. Пусть объект массы $m=1000$ кг требуется разогнать до скорости $\vartheta=0,5$ км/с. Найдите начальную массу фотонной ракеты $m_0$.
комментарий/решение

Классическая ракета Пусть ракета имеет начальную массу $m_0$, а скорость истечения топлива относительно ракеты постоянна и равна $u$. Считайте пока, что в начальный момент времени ракета покоится в лабораторной системе отсчета и внешние силы отсутствуют.
1. [0.5 балла] Найдите зависимость скорости ракеты $\vartheta$ от ее массы $m$. Эта формула называется формулой Циолковского. Ответ выразите через $m$, $m_0$, $u$.
2. [0.5 балла] Пусть объект массы $m=1000$ кг требуется разогнать до первой космической скорости. Найдите начальную массу ракеты $m_0$ с топливом, если $u=5$ км/с, ускорение свободного падения $g=9,8$ м/с$^2$, радиус Земли $R=6400$ км.
Пусть ракета движется в поле тяжести Земли, ускорение свободного падения $g$ которого будем считать постоянным, а расход топлива $\mu(t)=-dm(t)/dt$ может зависеть от времени.
3. [0.75 балла] Запишите уравнение движения ракеты в гравитационном поле Земли. Это уравнение называется уравнением Мещерского. Ответ выразите через $m$, $v$, $u$, $g$, $\mu$.
Далее считайте, что скорость истечения топлива $u$ направлена вдоль ускорения свободного падения $g$, а начальная скорость ракеты равна нулю.
4. [0.75 балла] Найдите, как расход топлива $\mu_{st}(t)$ должен зависеть от времени $t$, чтобы ракета висела на одной высоте неподвижно. Ответ выразите через $m_0$, $u$, $g$, $t$. Пусть теперь расход топлива постоянен во времени и равен $\mu$, причем всегда $\mu>\mu_{st}(t)$.
5. [2.0 балла] Тогда зависимость скорости ракеты $\vartheta(t)$ от времени $t$. может быть представлена в виде $$v(t)=A_1t+A_2ln(1+A_3t),$$ где $A_1$, $A_2$, $A_3$ — некоторые постоянные. Найдите $A_1$, $A_2$, $A_3$ и выразите их через $m_0$, $u$, $g$, $\mu$.
6. [1.0 балла] Пусть начальная масса ракеты равна $m_0$, а конечная масса — $m$. Найдите максимальную высоту $H_{\max}$, которую может достигнуть ракета и соответствующий расход топлива $\mu_{opt}$. Ответ выразите через $m_0$, $m$, $u$, $g$. Релятивистская ракета
В предыдущей части считалось, что ракета движется с нерелятивистской скоростью. Для осуществления межзвездных путешествий необходимо разгонять ракеты до скоростей, близких к скорости света и тогда в расчетах нельзя пренебрегать эффектами теории относительности. Для установления характера движения ракеты в релятивистском случае введем понятие сопутствующей системы отсчета. Сопутствующая система отсчета — это инерциальная система отсчета, которая движется относительно лабораторной системы отсчета со скоростью самой ракеты, то есть это система отсчета, в которой ракета в данный момент времени покоится.
7. [2.5 балла] Найдите связь ускорения ракеты в сопутствующей системе отсчета $a_{p}$ с ее ускорением в лабораторной системе отсчета $a_{r}$, если скорость ракеты в данный момент времени равна $v$, а скорость света — $c$. Ответ выразите через $a_{p}$, $a_{r}$, $v$, $c$.
8. [1.5 балла] Пусть ракета в начальный момент времени покоится. Тогда используя результаты предыдущего пункта можно показать, что масса ракеты в некоторый момент времени в сопутствующей системе отсчета связана с ее скоростью в лабораторной системе соотношением $$m=m_0\left(\frac{1-v/c}{1+v/c}\right)^{\alpha}.$$ Найдите $\alpha$ и выразите его через $u$, $c$.
9. [0.25 балла] Пусть объект массы $m=1000$ кг требуется разогнать до скорости $\vartheta=0,5$ с, равной половине скорости света $c=3\cdot 10^8$ м/с. Найдите начальную массу ракеты $m_0$ с топливом в виде степени с основанием $10$, если скорость истечения топлива $u=5$ км/с,
10. [0.25 балла] С точки зрения практики наилучшей является так называемая фотонная ракета, которая выбрасывает назад не раскаленные газы, получаемые при сгорании топлива, а фотоны. Пусть объект массы $m=1000$ кг требуется разогнать до скорости $\vartheta=0,5$ км/с. Найдите начальную массу фотонной ракеты $m_0$.
комментарий/решение
Задача №3. Метаматериалы (10 баллов)
1. [1.0 балла] Найдите аналитическую формулу для полного сопротивления проводника $R_0$ и рассчитайте его численное значение; По проводнику пропускают ток силой $I=1$ А. Известно, что теплообмен с окружающей средой происходит по закону Ньютона-Рихмана $$P_{\text{est}}=\alpha(T_{s}-T_{0}),$$ где $P_{\text{est}}$ — мощность потерь с единицы поверхности проводника с температурой поверхности $T_{s}$, $T_0=293$ К — температура окружающей среды, $\alpha$ — некоторая постоянная, называемая коэффициентом теплоотдачи.
2. [1.0 балла] Найдите аналитическую формулу для температуры поверхности проводника $T_{s}$ и рассчитайте ее численное значение; Температура проводника меняется с глубиной вследствие явления теплопроводности, которое описывается следующим законом Фурье $$P=-kS\frac{\Delta T}{\Delta x},$$ где $P$ — мощность теплового потока между гранями параллелепипеда площадью $S$, $\Delta T$ — перепад температур между гранями параллелепипеда, расположенными на расстоянии $\Delta x$ друг от друга, $k$ — коэффициент теплопроводности.
3. [2.5 балла] Найдите аналитическую формулу для температуры в центре проводника $T_{\max}$ и рассчитайте ее численное значение;
4. [0.5 балла] Найдите аналитическую формулу для изменения радиуса проводника $\delta R_{T}$, обусловленного тепловым расширением, и рассчитайте его численное значение; Внимание! В дальнейших расчетах считайте проводник бесконечно длинным.
5. [0.5 балла] Найдите зависимость индукции магнитного поля $B(r)$ внутри проводника в зависимости от расстояния $r$ до его оси;
6. [1.0 балла] Найдите аналитическую формулу для энергии магнитного поля $W_{B}$ внутри проводника и рассчитайте ее численное значение;
7. [1.0 балла] В результате пропускания электрического тока по проводнику в нем возникает механическое напряжение. Найдите зависимость давления $p(r)$ внутри проводника в зависимости от расстояния $r$ до его оси;
8. [1.0 балла] Найдите аналитическую формулу для механической энергии деформаций проводника $W_{\sigma}$ и рассчитайте ее численное значение;
9. [1.0 балла] Найдите аналитическую формулу для изменения радиуса проводника $\sigma W_{\sigma}$, обусловленного механическими напряжениями, и рассчитайте его численное значение;
10. [0.5 балла] Найдите величину коэффициента теплового расширения $\gamma$, при которой радиус проводника не изменился бы при пропускании через него электрического тока. Справка. Значение магнитной постоянной равно $\mu_0=4\pi \cdot 10^{-7}$ Гн/м.
комментарий/решение


1. [1.0 балла] Найдите аналитическую формулу для полного сопротивления проводника $R_0$ и рассчитайте его численное значение; По проводнику пропускают ток силой $I=1$ А. Известно, что теплообмен с окружающей средой происходит по закону Ньютона-Рихмана $$P_{\text{est}}=\alpha(T_{s}-T_{0}),$$ где $P_{\text{est}}$ — мощность потерь с единицы поверхности проводника с температурой поверхности $T_{s}$, $T_0=293$ К — температура окружающей среды, $\alpha$ — некоторая постоянная, называемая коэффициентом теплоотдачи.
2. [1.0 балла] Найдите аналитическую формулу для температуры поверхности проводника $T_{s}$ и рассчитайте ее численное значение; Температура проводника меняется с глубиной вследствие явления теплопроводности, которое описывается следующим законом Фурье $$P=-kS\frac{\Delta T}{\Delta x},$$ где $P$ — мощность теплового потока между гранями параллелепипеда площадью $S$, $\Delta T$ — перепад температур между гранями параллелепипеда, расположенными на расстоянии $\Delta x$ друг от друга, $k$ — коэффициент теплопроводности.
3. [2.5 балла] Найдите аналитическую формулу для температуры в центре проводника $T_{\max}$ и рассчитайте ее численное значение;
4. [0.5 балла] Найдите аналитическую формулу для изменения радиуса проводника $\delta R_{T}$, обусловленного тепловым расширением, и рассчитайте его численное значение; Внимание! В дальнейших расчетах считайте проводник бесконечно длинным.
5. [0.5 балла] Найдите зависимость индукции магнитного поля $B(r)$ внутри проводника в зависимости от расстояния $r$ до его оси;
6. [1.0 балла] Найдите аналитическую формулу для энергии магнитного поля $W_{B}$ внутри проводника и рассчитайте ее численное значение;
7. [1.0 балла] В результате пропускания электрического тока по проводнику в нем возникает механическое напряжение. Найдите зависимость давления $p(r)$ внутри проводника в зависимости от расстояния $r$ до его оси;
8. [1.0 балла] Найдите аналитическую формулу для механической энергии деформаций проводника $W_{\sigma}$ и рассчитайте ее численное значение;
9. [1.0 балла] Найдите аналитическую формулу для изменения радиуса проводника $\sigma W_{\sigma}$, обусловленного механическими напряжениями, и рассчитайте его численное значение;
10. [0.5 балла] Найдите величину коэффициента теплового расширения $\gamma$, при которой радиус проводника не изменился бы при пропускании через него электрического тока. Справка. Значение магнитной постоянной равно $\mu_0=4\pi \cdot 10^{-7}$ Гн/м.
комментарий/решение