6-я Жаутыковская олимпиада (2010), теоретический тур
Есеп №1. Эта задача состоит из трех частей, не связанных друг с другом.
1А (3 балла) Один конец однородного твердого стержня массой $m$ и длиной $l$ подвешен к вертикальной опоре с помощью идеального шарнира, а второй подвешен на нити, так что стержень находится в горизонтальном положении. В некоторый момент времени нить перерезают. Найти силу реакции опоры в шарнире в зависимости от угла отклонения стержня от горизонтального положения.
1В (4 балла) Плотность слоя жидкости высотой $H$, заполняющей полностью закрытый толстостенный цилиндрический сосуд, линейно уменьшается с высотой от $\rho_{\max}$ до малой величины, которую можно принять равной нулю. Над жидкостью находится тонкий слой насыщенного пара, давлением которого можно пренебречь по сравнению с гидростатическим давлением жидкости. Снизу в жидкость погружают перевернутую пробирку объемом $V_0$, масса $M$ которой сосредоточена возле горлышка, а длина значительно меньше $H$. В пробирке находится газ, занимающий объем $V_1$, масса которого значительно меньше массы пробирки. Температура системы поддерживается постоянной. Может ли пробирка неподвижно зависнуть в сосуде? Если да, то при каких условиях и на какой высоте от дна? Будет ли ее положение равновесия устойчивым? Объем стенок пробирки мал по сравнению с $V_1$.
1C (3 балла) На потолке комнаты высотой $L=3$м расположен плоский матовый светильник, имеющий форму прямоугольника размерами $c\times b$. Под светильником на высоте $h$ над полом горизонтально расположили непрозрачную квадратную пластинку со стороной $a=10$см (см. рис.1). На рис.2 схематически изображен вид тени, отбрасываемой пластинкой на пол комнаты: тень состоит из темного прямоугольника, окруженного другим более светлым прямоугольником, причем при приближении к краям этого внешнего прямоугольника тень светлеет. Цена деления шкал на этом рисунке 1,0 см. Определите размеры источника света $b$ и $c$, и высоту $h$ над полом, на которой расположена пластинка. Укажите ориентацию источника света по отношению к тени, отбрасываемой пластинкой.
комментарий/решение
1А (3 балла) Один конец однородного твердого стержня массой $m$ и длиной $l$ подвешен к вертикальной опоре с помощью идеального шарнира, а второй подвешен на нити, так что стержень находится в горизонтальном положении. В некоторый момент времени нить перерезают. Найти силу реакции опоры в шарнире в зависимости от угла отклонения стержня от горизонтального положения.
1В (4 балла) Плотность слоя жидкости высотой $H$, заполняющей полностью закрытый толстостенный цилиндрический сосуд, линейно уменьшается с высотой от $\rho_{\max}$ до малой величины, которую можно принять равной нулю. Над жидкостью находится тонкий слой насыщенного пара, давлением которого можно пренебречь по сравнению с гидростатическим давлением жидкости. Снизу в жидкость погружают перевернутую пробирку объемом $V_0$, масса $M$ которой сосредоточена возле горлышка, а длина значительно меньше $H$. В пробирке находится газ, занимающий объем $V_1$, масса которого значительно меньше массы пробирки. Температура системы поддерживается постоянной. Может ли пробирка неподвижно зависнуть в сосуде? Если да, то при каких условиях и на какой высоте от дна? Будет ли ее положение равновесия устойчивым? Объем стенок пробирки мал по сравнению с $V_1$.
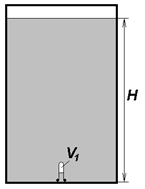
1C (3 балла) На потолке комнаты высотой $L=3$м расположен плоский матовый светильник, имеющий форму прямоугольника размерами $c\times b$. Под светильником на высоте $h$ над полом горизонтально расположили непрозрачную квадратную пластинку со стороной $a=10$см (см. рис.1). На рис.2 схематически изображен вид тени, отбрасываемой пластинкой на пол комнаты: тень состоит из темного прямоугольника, окруженного другим более светлым прямоугольником, причем при приближении к краям этого внешнего прямоугольника тень светлеет. Цена деления шкал на этом рисунке 1,0 см. Определите размеры источника света $b$ и $c$, и высоту $h$ над полом, на которой расположена пластинка. Укажите ориентацию источника света по отношению к тени, отбрасываемой пластинкой.
комментарий/решение
Есеп №2. Опыт Толмена и Стюарта (10 баллов)
В 1916 году Толмен и Стюарт поставили знаменитый опыт, подтверждающий, что ток в металлах обусловлен движением свободных электронов. Схема опыта изображена на рисунке слева.
Очень длинная катушка имеет собственный момент инерции $J_0$, радиус $r$ и длину $h$. На катушку намотан один слой тонкого металлического провода, имеющего длину $l$, массу $m$, число витков на единицу длины равно $n$. Концы провода с помощью скользящих контактов замкнуты на гальванометр. Катушка с проводом приводится в быстрое вращение с угловой скоростью $\omega_0$, а затем останавливается трением с моментом силы $M$. Полное сопротивление цепи равно $R$, а ее емкостью можно пренебречь.
Часть 1. В этой части полностью пренебрегается индуктивностью катушки и предполагается выполнение закона Ома в любой момент времени. Дайте ответы на следующие вопросы:
комментарий/решение
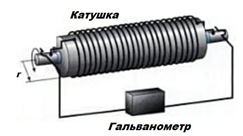
В 1916 году Толмен и Стюарт поставили знаменитый опыт, подтверждающий, что ток в металлах обусловлен движением свободных электронов. Схема опыта изображена на рисунке слева.
Очень длинная катушка имеет собственный момент инерции $J_0$, радиус $r$ и длину $h$. На катушку намотан один слой тонкого металлического провода, имеющего длину $l$, массу $m$, число витков на единицу длины равно $n$. Концы провода с помощью скользящих контактов замкнуты на гальванометр. Катушка с проводом приводится в быстрое вращение с угловой скоростью $\omega_0$, а затем останавливается трением с моментом силы $M$. Полное сопротивление цепи равно $R$, а ее емкостью можно пренебречь.
Часть 1. В этой части полностью пренебрегается индуктивностью катушки и предполагается выполнение закона Ома в любой момент времени. Дайте ответы на следующие вопросы:
- [1 балл] Определите полный момент инерции $J$ катушки с проводом. Ответ выразите через $J_0$, $M$, $\omega_0$.
- [1 балл] Определите зависимость угловой скорости вращения катушки $\omega(t)$ от времени $t$. Ответ выразите через $J$, $M$, $\omega_0$.
- [1 балл] Определите зависимость силы тока в цепи катушки $I(t)$ от времени $t$. Ответ выразите через $J$, $M$, $r$, $l$, $R$ и $m_{e}$, $e$ — массу и заряд электрона, соответственно.
- [2 балла] Гальванометр зафиксировал протекший через него электрический заряд $Q$. Выразите отношение заряда электрона к его массе $e/m_{e}$ через $\omega_0$, $r$, $l$, $R$, $Q$.
- [1 балл] Найдите максимальное значение тока $I_{\max}$ в катушке. Ответ выразите через $J$, $M$, $r$, $l$, $R$ и $m_{e}$, $e$. Изобразите примерный график зависимости $I(t)$.
- [1 балл] Найдите максимальную энергию $W_0$, запасенную в катушке. Ответ выразите через $J$, $M$, $r$, $l$, $R$ и $m_{e}$, $e$, $n$, $h$ и магнитную постоянную $\mu_0$.
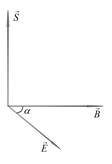
- [3 балла] Поток $S$ электромагнитной энергии через единицу площади поверхности определяется вектором Пойнтинга, который перпендикулярен электрическому и магнитному полю и равен по модулю $S=\frac{1}{\mu_{0}}EB \sin\alpha$, где $E$ — вектор напряженности электрического поля, $B$ — вектор магнитной индукции, а $\alpha$ — угол между ними (смотрите рисунок справа). Определите электромагнитную энергию $W$, проходящую через боковую поверхность катушки за время нарастания тока, и электромагнитную энергию $W'$, проходящую через боковую поверхность за время убывания тока. Ответ выразите через $l$, $r$, $M$, $J$, $n$, $R$, $m_{e}$, $e$, $\mu_0$.
Часть 2. В этой части необходимо учесть малую индуктивность катушки, которая считается очень длинной, так что краевыми эффектами можно пренебречь. Дайте ответы на следующие вопросы:
комментарий/решение
Есеп №3. Реликтовое излучение и космические лучи (10 баллов)
Согласно современной космологии, наша Вселенная наполнена электромагнитным излучением, оставшимся после Большого взрыва. Это излучение называется реликтовым. С хорошей точностью реликтовое излучение однородно и изотропно в системе отсчета, свя-занной с нашей Галактикой, которую в дальнейшем будем считать лабораторной системой отсчета, а распределение по частотам интенсивности этого излучения совпадает со спектром абсолютно черного тела при температуре $T=2,7$ К. Работы по открытию и исследованию свойств реликтового излучения отмечены Нобелевскими премиями по физике в 1978 и 2006 годах.
Реликтовые фотоны чрезвычайно многочисленны и поэтому могут влиять на имеющееся в Галактике излучение другой природы - космические лучи (КЛ). Считается, что КЛ образуются при взрывах звезд. КЛ состоят в основном из протонов, их энергия может превышать на много порядков энергии, доступные на земных ускорителях. Механизм генерации КЛ сверхвысоких энергий не вполне ясен, однако экспериментально наблюдаемое распределение по энергии КЛ ограничено сверху величиной $E^{\max}_{p}=10^{21}$ $eV$. В данной задаче предполагается, что это ограничение обусловлено потерями энергии при взаимодействии протонов с реликтовым излучением. Протоны могут участвовать в комптоновском рассеянии $$p+\gamma \to p+\gamma, \quad (1)$$ и вызвать реакцию $$p + \gamma \to \bigtriangleup \to \pi^0 +p, \quad (2)$$ где $p$ — протон, $\gamma$ — реликтовый фотон, $\bigtriangleup$ — самый легкий по сравнению с нуклоном барион с массой покоя $m_{\bigtriangleup}=1,232\times 10^6$ $eV/c^2$, который быстро распадается на пимезон $\pi^0$ и протон $p$. ($\bigtriangleup$ — частица распадется также на $\pi^{+}$ — мезон и нейтрон. Нейтрон довольно быстро превращается в протон за счет $\beta$ -распада, поэтому явный учет этого канала реакции не имеет принципиального значения в данной задаче). За счет рождения $\bigtriangleup$ -частицы вероятность взаимодействия протона с -квантом резко возрастает.
Цель данной задачи — определить верхнюю границу наблюдаемого энергетического спектра КЛ, предполагая, что реакция (2) является основным механизмом потерь энергии КЛ, и сравнить потери энергии протоном в реакциях (1) и (2).
В следующих заданиях энергию измерять в электрон-вольтах $eV$, а импульсы — в $eV/c$, где $c$ — скорость света в вакууме. Масса покоя протона $m_p=938\times 10^6$ $eV/c^2$, масса покоя пимезона $m_{\pi}=140\times 10^6$ $eV/c^2$. Постоянная Больцмана $k=1,38\times 10^{-23}$ Дж$\cdot$ К$^{-1}$.
комментарий/решение
Согласно современной космологии, наша Вселенная наполнена электромагнитным излучением, оставшимся после Большого взрыва. Это излучение называется реликтовым. С хорошей точностью реликтовое излучение однородно и изотропно в системе отсчета, свя-занной с нашей Галактикой, которую в дальнейшем будем считать лабораторной системой отсчета, а распределение по частотам интенсивности этого излучения совпадает со спектром абсолютно черного тела при температуре $T=2,7$ К. Работы по открытию и исследованию свойств реликтового излучения отмечены Нобелевскими премиями по физике в 1978 и 2006 годах.
Реликтовые фотоны чрезвычайно многочисленны и поэтому могут влиять на имеющееся в Галактике излучение другой природы - космические лучи (КЛ). Считается, что КЛ образуются при взрывах звезд. КЛ состоят в основном из протонов, их энергия может превышать на много порядков энергии, доступные на земных ускорителях. Механизм генерации КЛ сверхвысоких энергий не вполне ясен, однако экспериментально наблюдаемое распределение по энергии КЛ ограничено сверху величиной $E^{\max}_{p}=10^{21}$ $eV$. В данной задаче предполагается, что это ограничение обусловлено потерями энергии при взаимодействии протонов с реликтовым излучением. Протоны могут участвовать в комптоновском рассеянии $$p+\gamma \to p+\gamma, \quad (1)$$ и вызвать реакцию $$p + \gamma \to \bigtriangleup \to \pi^0 +p, \quad (2)$$ где $p$ — протон, $\gamma$ — реликтовый фотон, $\bigtriangleup$ — самый легкий по сравнению с нуклоном барион с массой покоя $m_{\bigtriangleup}=1,232\times 10^6$ $eV/c^2$, который быстро распадается на пимезон $\pi^0$ и протон $p$. ($\bigtriangleup$ — частица распадется также на $\pi^{+}$ — мезон и нейтрон. Нейтрон довольно быстро превращается в протон за счет $\beta$ -распада, поэтому явный учет этого канала реакции не имеет принципиального значения в данной задаче). За счет рождения $\bigtriangleup$ -частицы вероятность взаимодействия протона с -квантом резко возрастает.
Цель данной задачи — определить верхнюю границу наблюдаемого энергетического спектра КЛ, предполагая, что реакция (2) является основным механизмом потерь энергии КЛ, и сравнить потери энергии протоном в реакциях (1) и (2).
В следующих заданиях энергию измерять в электрон-вольтах $eV$, а импульсы — в $eV/c$, где $c$ — скорость света в вакууме. Масса покоя протона $m_p=938\times 10^6$ $eV/c^2$, масса покоя пимезона $m_{\pi}=140\times 10^6$ $eV/c^2$. Постоянная Больцмана $k=1,38\times 10^{-23}$ Дж$\cdot$ К$^{-1}$.
- [0.5 балла] Оцените наиболее вероятную энергию $E_{\gamma}$ и соответствующий импульс $p_{\gamma}$ реликтовых фотонов, учитывая, что они соответствуют излучению черного тела при температуре $T=2,7$ К.
- [1 балл] Масса покоя частицы $m$ связана с полной релятивистской энергией $E$ и импульсом $\overline{p}$ этой частицы в произвольной инерциальной системе отсчета соотношением $E^2/c^2 - \overline{p}^2=m^2 c^2$. Здесь величина $mc^2$ не зависит от системы отсчета и является полной внутренней энергией частицы. Выразить полную внутреннюю энергию двух невзаимодействующих частиц с массами покоя $m_1$, $m_2$ (т.е. полную энергию в системе отсчета, в которой полный импульс физической системы равен нулю) через энергии $E_1$, $E_2$, и импульсы $\overline{p_1}^2$, $\overline{p_2}^2$ этих частиц в произвольной системе отсчета.
- Определите, при какой наименьшей энергии протона возможна реакция (2):
- [1 балл] Предполагая, что в системе Галактики протон имеет максимальную энергию $E_{p}^{\max}$ и сталкивается с летящим ему навстречу реликтовым фотоном, определите импульс $\pi^0$-мезона в реакции (2) в этой же системе отсчета для случая, когда вылетающие частицы движутся по или против направления начального импульса протона. Насколько при этом изменяется импульс протона?
- [1.5 балла] Какова величина импульса вылетающего фотона в комптоновском рассеянии (1) при тех же условиях, что и в пункте 4?
- [1 балл] Возможна ли реакция (2) с реликтовым излучением, если в системе Галактики начальные импульсы протона и фотона направлены в одну сторону? Если реакция воз-можна, то какова при этом должна быть минимальная величина начального импульса фотона в системе Галактики?
В следующих заданиях предполагайте, что начальный фотон в реакциях (1) и (2) имеет найденные Вами значения энергии и импульса.
Для дальнейшего анализа может понадобиться релятивистский закон преобразования импульса и энергии частицы. При переходе из инерциальной системы отсчета $S$ в инерциальную систему $S'$, движущуюся относительно первой со скоростью $\vartheta_0$ вдоль положительного направления оси $Z(OZ \uparrow \uparrow OZ)$, импульс и энергия преобразуются так же как координаты пространственно-временной точки $(x,y,z,t) \to (x',y',z',t')$: $$p_{z}c=G\left(p_{z}'c+\frac{\vartheta_0}{c}E'\right),$$ $$p_{x}=p_{x}',$$ $$p_{y}=p_{y}',$$ $$E=G\left( E'c+\frac{\vartheta_0}{c}p_{z}' c\right). \quad (3)$$ Здесь $$E'/c=\sqrt{m^2c^2+p_{x}'^2+p_{y}'^2+p_{z}'^2}, G=1/\sqrt{1-(V/c)^2}.$$
a) [2 балла] в системе центра масс протона и фотона $p+\gamma$ (то есть в системе отсчета, в которой суммарный импульс протона и фотона равен нулю);
b) [3 балла] в системе Галактики.
Исходя из полученных результатов, определите максимальную энергию протонов в спектре КЛ.
комментарий/решение