Районная олимпиада, 2025-2026 учебный год, 10 класс
Есеп №1. $a+b=1$ болатын теріс емес $a, b$ нақты сандары берілген. Дәлелдеңіз: $$\frac{a^2+b^2}{2} \le a^3+b^3 \le a^2+b^2 .$$
комментарий/решение(2)
комментарий/решение(2)
Есеп №2. $a^2=b(b+5)-2$ теңдеуін қанағаттандыратын барлық $(a, b)$ натурал сандар жұптарын табыңыз.
комментарий/решение(2)
комментарий/решение(2)
Есеп №3. a) Ең кіші ортақ еселігі $15$-ке тең болатын, $\text{ЕКОЕ}[m, n] = 15$ барлығы қанша $(m, n)$ натурал сандар жұбы бар?
b) Ең кіші ортақ еселігі $2025$-ке тең болатын, $\text{ЕКОЕ}[m, n] = 2025$ барлығы қанша $(m, n)$ натурал сандар жұбы бар?
комментарий/решение(1)
b) Ең кіші ортақ еселігі $2025$-ке тең болатын, $\text{ЕКОЕ}[m, n] = 2025$ барлығы қанша $(m, n)$ натурал сандар жұбы бар?
комментарий/решение(1)
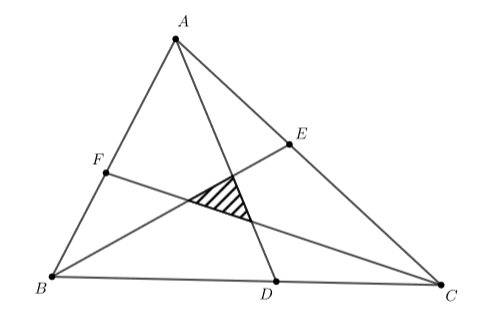
Есеп №4. $ABC$ үшбұрышының $BC$, $CA$ және $AB$ қабырғаларында, $BD:DC = CE:EA = AF:FB = 3:2$ қатынастары орындалатындай, сәйкесінше $D$, $E$ және $F$ нүктелері жатыр (суретте көрсетілгендей). Егер боялған бөліктің ауданы $100$-ге тең болса, онда $ABC$ үшбұрышының ауданы қаншаға тең?
комментарий/решение(2)
комментарий/решение(2)