Районная олимпиада, 2025-2026 учебный год, 10 класс
Задача №1. Даны неотрицательные действительные числа $a, b$ для которых $a+b=1$. Докажите, что $$\frac{a^2+b^2}{2} \le a^3+b^3\le a^2+b^2 .$$
комментарий/решение(2)
комментарий/решение(2)
Задача №2. Найдите все пары натуральных чисел $(a, b)$, удовлетворяющих уравнению $a^2=b(b+5)-2$.
комментарий/решение(2)
комментарий/решение(2)
Задача №3. a) Сколько всего пар натуральных чисел $(m, n)$ существует таких, что их наименьшее общее кратное равно $15$, то есть $\text{НОК}[m, n] = 15$?
b) Сколько всего пар натуральных чисел $(m, n)$ существует таких, что их наименьшее общее кратное равно $2025$, то есть $\text{НОК}[m, n] = 2025$?
комментарий/решение(1)
b) Сколько всего пар натуральных чисел $(m, n)$ существует таких, что их наименьшее общее кратное равно $2025$, то есть $\text{НОК}[m, n] = 2025$?
комментарий/решение(1)
Задача №4. В треугольнике $ABC$ точки $D$, $E$ и $F$ лежат на сторонах $BC$, $CA$ и $AB$ соответственно, так что $BD:DC = CE:EA = AF:FB = 3:2$, как показано на рисунке. Если площадь заштрихованной области равна 100, какова площадь треугольника $ABC$?
комментарий/решение(2)
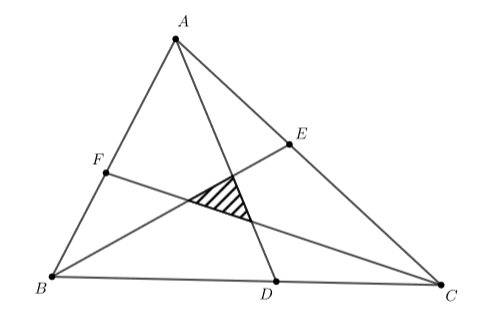
комментарий/решение(2)