Юниорская олимпиада по математике. Районный этап. 2023-2024 учебный год. 7 класс.
Есеп №1. Бір мезетте 4, 6 және 9-ға бөлінетін екі таңбалы неше сан бар?
A) 1
B) 2
C) 3
D) 4
E) 5
комментарий/решение
A) 1
B) 2
C) 3
D) 4
E) 5
комментарий/решение
Есеп №2. 18 санын $x\cdot y \cdot z$ көбейтіндісі түрінде әртүрлі қанша тәсілмен жазуға болады, бұл жерде $x$, $y$ және $z$ — натурал сандар.
A) 6
B) 36
C) 12
D) 18
E) 9
комментарий/решение
A) 6
B) 36
C) 12
D) 18
E) 9
комментарий/решение
Есеп №3. Бірінші аялдамада бос автобусқа 25 жолаушы отырды. Содан әр аялдамада 5 адам түсіп, 8 адам отырды. Төртінші және бесінші аялдамалар арасында автобуста қанша жолаушы болды?
A) 40
B) 23
C) 31
D) 27
E) 34
комментарий/решение
A) 40
B) 23
C) 31
D) 27
E) 34
комментарий/решение
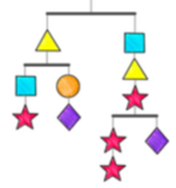
Есеп №4. Таразы тепе-теңдікте тұр. Шаршы жұлдыздан неше есе ауыр?
A) 5
B) 4
C) 3
D) 2
E) 6
комментарий/решение
A) 5
B) 4
C) 3
D) 2
E) 6
комментарий/решение
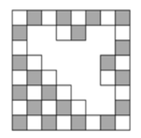
Есеп №5. Термиттер ескі ағаш шахмат тақтасының бір бөлігін жеді. Олар қанша қара торкөзін жеді?
A) 10
B) 11
C) 12
D) 13
E) 9
комментарий/решение
A) 10
B) 11
C) 12
D) 13
E) 9
комментарий/решение
Есеп №6. Асханада Әйгерім, Бақытжан, Ғалия, Дәулет, Ермек деген бес оқушы кезекте тұр.
Кезектің басында Бақытжан тұр.
Ғалым Дәулеттің қасында емес, Әйгерімнің қасында тұр.
Әйгерім, Бақытжан мен Дәулеттің ешқандай екеуі қатар тұрған жоқ.
Ермектің қасында кім тұр?
A) Әйгерім және Бақытжан / Айгерим и Бахытжан
B) Әйгерім және Даулет / Айгерим и Даулет
C) Ғалия және Бақытжан / Галия и Бахытжан
D) Ғалия және Даулет / Галия и Даулет
E) Бақытжан және Даулет / Бахытжан и Даулет
комментарий/решение
Кезектің басында Бақытжан тұр.
Ғалым Дәулеттің қасында емес, Әйгерімнің қасында тұр.
Әйгерім, Бақытжан мен Дәулеттің ешқандай екеуі қатар тұрған жоқ.
Ермектің қасында кім тұр?
A) Әйгерім және Бақытжан / Айгерим и Бахытжан
B) Әйгерім және Даулет / Айгерим и Даулет
C) Ғалия және Бақытжан / Галия и Бахытжан
D) Ғалия және Даулет / Галия и Даулет
E) Бақытжан және Даулет / Бахытжан и Даулет
комментарий/решение
Есеп №7. Суретте көрсетілген бұрыш пішіндердің ең аз санын қолданып шаршы құрастырып шығаруыңыз керек. Жауабыңызда пайдаланылған «бұрыштар» санын көрсетіңіз.
A) 3
B) 16
C) 12
D) 27
E) 21
комментарий/решение

A) 3
B) 16
C) 12
D) 27
E) 21
комментарий/решение
Есеп №8. 5 әртүрлі натурал сандардың қосындысы 35-ке тең және бұл сандардың ең кішісі олардың ең үлкенінің жартысынан үлкен екені белгілі. Осы сандардың ең үлкен санын табыңыз.
A) 11
B) 8
C) 10
D) 9
E) 6
комментарий/решение
A) 11
B) 8
C) 10
D) 9
E) 6
комментарий/решение
Есеп №9. Егер пирамиданы жалғастырсақ, онда 101 саны нешінші қатарда кездеседі?
A) 13
B) 10
C) 9
D) 12
E) 11
комментарий/решение

A) 13
B) 10
C) 9
D) 12
E) 11
комментарий/решение
Есеп №10. Футбол чемпионатына 16 команда қатысты. Әр команда әр командамен бір рет ойнады. Команда жеңіс үшін 3 ұпай, тең ойын үшін 1 ұпай, жеңіліс үшін 0 ұпай алады. Турнир қорытындысы бойынша барлық командалар жалпы 350 ұпай жинады. Қанша ойын тең аяқталды?
A) 10
B) 11
C) 12
D) 13
E) 14
комментарий/решение
A) 10
B) 11
C) 12
D) 13
E) 14
комментарий/решение
Есеп №11. $a$ және $b$ оң сандары үшін $a \oplus b=a-\frac{1}{b}$ операциясы берілген. $2\oplus(2\oplus 2)$ өрнегінің мәні нешеге тең?
A) $\frac{2}{3}$
B) 1
C) $\frac{4}{3}$
D) 2
E) $\frac{3}{4}$
комментарий/решение
A) $\frac{2}{3}$
B) 1
C) $\frac{4}{3}$
D) 2
E) $\frac{3}{4}$
комментарий/решение
Есеп №12. Қызыл раушан гүлі 3000 теңге, ал ақ раушан гүлі 2000 теңге тұрады. 50000 теңге тұратын гүл шоғын неше түрлі тәсілмен жасауға болады, егер гүл шоғындағы гүлдер саны тақ болуы керек болса?
A) 9
B) 5
C) 8
D) 7
E) 10
комментарий/решение
A) 9
B) 5
C) 8
D) 7
E) 10
комментарий/решение
Есеп №13. Төртбұрыш пен шеңбер ең көп дегенде неше нүктеде қиылыса алады?
A) 9
B) 7
C) 6
D) 8
E) 5
комментарий/решение
A) 9
B) 7
C) 6
D) 8
E) 5
комментарий/решение
Есеп №14. Шегіртке 15 секундта 6 рет секіреді. Әрбір секіріс 6 см құрайды. Түзу бойымен 40 секунд секіргеннен кейін шегіртке тоқтайды. Шегіртке қанша қашықтыққа (сантиметрмен) секірді?
A) 84 см
B) 108 см
C) 72 см
D) 96 см
E) 112 см
комментарий/решение
A) 84 см
B) 108 см
C) 72 см
D) 96 см
E) 112 см
комментарий/решение
Есеп №15. Үш жай сан берілген. Екінші сан біріншіден 27-ге көп, ал үшіншіден 14-ке аз. Осы жай сандардың қосындысы нешеге тең?
A) 76
B) 79
C) 74
D) 77
E) 78
комментарий/решение
A) 76
B) 79
C) 74
D) 77
E) 78
комментарий/решение
Есеп №16. Бөлмеде 10 адам бар. Олардың әркайсысы не үнемі шындықты айтатын сері, не үнемі өтірік айтатын өтірікші. Бөлмедегілердің бірі: «Бұл бөлмеде $k_1$ өтірікші бар», екіншісі: «Бұл бөлмеде $k_2$ өтірікші бар», $\ldots, 10$-шы: «Бұл бөлмеде $k_{10}$ өтірікші бар» деді. Барлық $k_1, k_2, \ldots, k_{10}$ сандары 10-нан аспайтыны белгілі. Олардың қосындысының мүмкін болатын ең үлкен мәні қандай?
A) 100
B) 99
C) 98
D) 90
E) 94
комментарий/решение
A) 100
B) 99
C) 98
D) 90
E) 94
комментарий/решение
Есеп №17. Қосындыны есептеңіз: $1 + 4 + 7 + \ldots + 2020 + 2023.$
A) 683100
B) 638100
C) 583100
D) 630100
E) 675100
комментарий/решение
A) 683100
B) 638100
C) 583100
D) 630100
E) 675100
комментарий/решение
Есеп №18. Мақсат пен оның сыныптастары жаңа фильмге билет алу үшін кинотеатрда 120 адамнан тұратын ұзын кезекте тұрады. Мақсат – сыныптастарының соңғысы және ұзын кезектің басынан санағанда 65-інші тұр. Дегенмен, кезектің басына ең жақын тұрған Мақсаттың сыныптасы Қайрат ұзын кезектің соңынан санағанда 73-інші орында тұр. Мақсаттың қанша сыныптасы бар?
A) 17
B) 18
C) 16
D) 19
E) 20
комментарий/решение
A) 17
B) 18
C) 16
D) 19
E) 20
комментарий/решение
Есеп №19. Ең болмағанда бір цифрасы тақ болатын неше төрт таңбалы сан бар?
A) 8250
B) 8375
C) 8500
D) 9000
E) 9425
комментарий/решение
A) 8250
B) 8375
C) 8500
D) 9000
E) 9425
комментарий/решение
Есеп №20. Қайрат шаршының ұяшықтарын әр жолда, әр бағанда және екі $3 \times 3$ диагоналда тұрған үш ұяшықтың түстері әртүрлі болатындай етіп бояғысы келеді. Бұлай бояу үшін Қайратқа ең аз дегенде неше түс қажет?
A) 6
B) 4
C) 3
D) 5
E) 9
комментарий/решение
A) 6
B) 4
C) 3
D) 5
E) 9
комментарий/решение
Есеп №21. Тақтаға 3, 4, 5, 6, 12 және 13 бүтін сандарын (әрбір сан бір-ақ рет қолданылды) қатар тұрған кез келген екі санның қосындысы толық квадрат болатындай етіп бір қатарға жазып шықты. Ортадағы екі санның қосындысын табыңыз.
A) 9
B) 25
C) 16
D) 18
E) 22
комментарий/решение
A) 9
B) 25
C) 16
D) 18
E) 22
комментарий/решение
Есеп №22. Төрт тізбектес тұрған жұп натурал санның көбейтіндісі $2^8 \cdot 3^2 \cdot 5 \cdot 11$ санына тең. Осы төрт санның қосындысы нешеге тең?
A) 84
B) 64
C) 68
D) 92
E) 76
комментарий/решение
A) 84
B) 64
C) 68
D) 92
E) 76
комментарий/решение
Есеп №23. Бірінші және соңғы цифрларының қосындысы 13-ке тең болатын, 1000-нан кіші неше натурал сан бар?
A) 60
B) 66
C) 57
D) 55
E) 63
комментарий/решение
A) 60
B) 66
C) 57
D) 55
E) 63
комментарий/решение
Есеп №24. Математикадан емтихан 20 есептен тұрады. Дұрыс жауап үшін студент 5 ұпай алады, дұрыс емес жауап үшін 1 ұпай шегеріледі, бос жауап үшін ұпай берілмейді. Іңкәр емтиханнан 31 ұпай алды. Ол жауап бере алатын есептердің ең көп саны қанша (дұрыс және бұрыс жауаптарды қоса санағанда)?
A) 16
B) 19
C) 17
D) 18
E) 20
комментарий/решение
A) 16
B) 19
C) 17
D) 18
E) 20
комментарий/решение
Есеп №25. Абзал мен Дарын бір зауытта жұмыс істейді. Әр тоғыз күн жұмыс істегеннен кейін Абзал бір күн демалады. Әр алты күн жұмыс істегеннен кейін Дарын бір күн демалады. Бүгін Абзалдың демалыс күні, ертең Дарынның демалыс күні. Бүгіннен бастап кем дегенде қанша күннен кейін олардың демалыс күндері бір күнде болады?
A) 47
B) 56
C) 40
D) 50
E) 53
комментарий/решение
A) 47
B) 56
C) 40
D) 50
E) 53
комментарий/решение
Есеп №26. 1, 1, 2, 3, 5, 8, 13, 21, 34, $\ldots$ Фибоначчи тізбегі берілген, яғни, үшінші саннан бастап, әр сан оның алдындағы екі санның қосындысына тең. 2023-інші орында тұрған санның соңғы цифрасын табыңыз.
A) 7
B) 5
C) 3
D) 9
E) 8
комментарий/решение
A) 7
B) 5
C) 3
D) 9
E) 8
комментарий/решение
Есеп №27. $ax+by=c$, $(a+2) x+(b-3) y=c+9$ және $(a+1) x+(b-1) y=c+2$ тендеулері аркылы берілген үш түзу бір $M$ нүктесінде киылысады. $M$ нүктесінің координаталарының қосындысы нешеге тең?
A) $-8$
B) 0
C) $-2$
D) 6
E) 4
комментарий/решение
A) $-8$
B) 0
C) $-2$
D) 6
E) 4
комментарий/решение
Есеп №28. Аспандағы жұлдыздардың саны $8 \times 12 + 98 \times 102 + 998 \times 1002 + \ldots + 99\ldots98 \times 100\ldots02$ санына тең. Соңғы қосылғыштағы $99\ldots98$ санында 9 цифрының 2023 данасы және $100\ldots 02$ санында 0 цифрының 2023 данасы бар. Жұлдыздар санының цифрларының қосындысы нешеге тең?
A) 2023
B) 2024
C) 2030
D) 2028
E) 2027
комментарий/решение
A) 2023
B) 2024
C) 2030
D) 2028
E) 2027
комментарий/решение
Есеп №29. $5\le x_1 \le x_2 \le x_3 \le x_4 \le 25$ болатындай етіп $x_1, x_2, x_3, x_4$ төрт натурал сандарды таңдадық және осы сандардың кез келген екеуі бір-бірінен кемінде 5-ке ерекшеленеді. Бұлай неше түрлі жолмен жасауға болады?
A) 84
B) 210
C) 126
D) 252
E) 148
комментарий/решение
A) 84
B) 210
C) 126
D) 252
E) 148
комментарий/решение
Есеп №30. $mn+m+n-53$ және $9n-6m+3$ өрнектерінің қосындысы мен айырмасы жай сандар болатындай $m$ және $n$ оң бүтін сандар алынған. $mn$ көбейтіндісін табыңыз.
A) 72
B) 48
C) 63
D) 44
E) 54
комментарий/решение
A) 72
B) 48
C) 63
D) 44
E) 54
комментарий/решение