Юниорская олимпиада по математике. Районный этап. 2023-2024 учебный год. 7 класс.
Задача №1. Сколько двузначных чисел делятся на 4, 6 и 9 одновременно?
A) 1
B) 2
C) 3
D) 4
E) 5
комментарий/решение
A) 1
B) 2
C) 3
D) 4
E) 5
комментарий/решение
Задача №2. Сколькими различными способами можно представить число в виде 18 произведения $x\cdot y \cdot z$, где $x$, $y$ и $z$ — натуральные числа.
A) 6
B) 36
C) 12
D) 18
E) 9
комментарий/решение
A) 6
B) 36
C) 12
D) 18
E) 9
комментарий/решение
Задача №3. На первой остановке в пустой автобус вошло 25 пассажиров. Потом на каждой остановке выходило 5 человек, а входило 8 человек. Сколько пассажиров ехало в автобусе между четвёртой и пятой остановками?
A) 40
B) 23
C) 31
D) 27
E) 34
комментарий/решение
A) 40
B) 23
C) 31
D) 27
E) 34
комментарий/решение
Задача №4. Весы находятся в равновесии. Во сколько квадрат тяжелее звезды?
A) 5
B) 4
C) 3
D) 2
E) 6
комментарий/решение
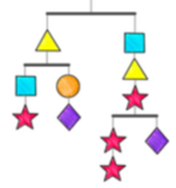
A) 5
B) 4
C) 3
D) 2
E) 6
комментарий/решение
Задача №5. Термиты съели кусок старой деревянной шахматной доски. Сколько чёрных клеток они съели?
A) 10
B) 11
C) 12
D) 13
E) 9
комментарий/решение
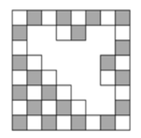
A) 10
B) 11
C) 12
D) 13
E) 9
комментарий/решение
Задача №6. В очереди в столовую стоят пять школьников: Айгерим, Бахытжан, Галия, Даулет и Ермек.
Бахытжан стоит в начале очереди.
Галым стоит рядом с Айгерим, но не рядом с Даулетом.
Никакие двое из Айгерим, Бахытжана и Даулета не стоят рядом.
Кто стоит рядом с Ермеком?
A) Әйгерім және Бақытжан / Айгерим и Бахытжан
B) Әйгерім және Даулет / Айгерим и Даулет
C) Ғалия және Бақытжан / Галия и Бахытжан
D) Ғалия және Даулет / Галия и Даулет
E) Бақытжан және Даулет / Бахытжан и Даулет
комментарий/решение
Бахытжан стоит в начале очереди.
Галым стоит рядом с Айгерим, но не рядом с Даулетом.
Никакие двое из Айгерим, Бахытжана и Даулета не стоят рядом.
Кто стоит рядом с Ермеком?
A) Әйгерім және Бақытжан / Айгерим и Бахытжан
B) Әйгерім және Даулет / Айгерим и Даулет
C) Ғалия және Бақытжан / Галия и Бахытжан
D) Ғалия және Даулет / Галия и Даулет
E) Бақытжан және Даулет / Бахытжан и Даулет
комментарий/решение
Задача №7. Сложите квадрат из наименьшего возможного количества «уголков», имеющих вид изображенный на рисунке. В ответе укажите количество использованных «уголков».
A) 3
B) 16
C) 12
D) 27
E) 21
комментарий/решение

A) 3
B) 16
C) 12
D) 27
E) 21
комментарий/решение
Задача №8. Сумма 5 различных натуральных чисел равна 35, причем известно, что наименьшее из этих чисел составляет больше половины от наибольшего из них. Найдите наибольшее из этих чисел.
A) 11
B) 8
C) 10
D) 9
E) 6
комментарий/решение
A) 11
B) 8
C) 10
D) 9
E) 6
комментарий/решение
Задача №9. Если продолжить пирамиду, то в каком ряду встретится число 101?
A) 13
B) 10
C) 9
D) 12
E) 11
комментарий/решение

A) 13
B) 10
C) 9
D) 12
E) 11
комментарий/решение
Задача №10. В чемпионате по футболу участвовало 16 команд. Каждая команда сыграла с каждой ровно один раз. За победу команда получала 3 очка,за ничью — 1 очко, за поражение — 0 очков. В конце турнира оказалось, что все команды в общем набрали 350 очков. Сколько игр окончилось ничьёй?
A) 10
B) 11
C) 12
D) 13
E) 14
комментарий/решение
A) 10
B) 11
C) 12
D) 13
E) 14
комментарий/решение
Задача №11. Для положительных чисел $a$ и $b$ введена опреция $a \oplus b=a-\frac{1}{b}$. Чему равно значение выражения $2\oplus(2\oplus 2)$?
A) $\frac{2}{3}$
B) 1
C) $\frac{4}{3}$
D) 2
E) $\frac{3}{4}$
комментарий/решение
A) $\frac{2}{3}$
B) 1
C) $\frac{4}{3}$
D) 2
E) $\frac{3}{4}$
комментарий/решение
Задача №12. Красная роза стоит 3000 тенге, а белая роза стоит тенге 2000. Сколькими различными способами можно составить букет стоимостью 50000 тенге, если в букете должно быть нечётное количество цветов?
A) 9
B) 5
C) 8
D) 7
E) 10
комментарий/решение
A) 9
B) 5
C) 8
D) 7
E) 10
комментарий/решение
Задача №13. Чему равно наибольшее количество точек пересечения четырёхугольника и окружности?
A) 9
B) 7
C) 6
D) 8
E) 5
комментарий/решение
A) 9
B) 7
C) 6
D) 8
E) 5
комментарий/решение
Задача №14. Кузнечик совершает 6 прыжков за 15 секунд. Каждый прыжок составляет 6 см. Через 40 секунд прыжка по прямой кузнечик останавливается. На какое расстояние (в сантиметрах) прыгнул кузнечик?
A) 84 см
B) 108 см
C) 72 см
D) 96 см
E) 112 см
комментарий/решение
A) 84 см
B) 108 см
C) 72 см
D) 96 см
E) 112 см
комментарий/решение
Задача №15. Даны три простых числа. Второе число на 27 больше первого и на 14 меньше третьего. Какова сумма этих простых чисел?
A) 76
B) 79
C) 74
D) 77
E) 78
комментарий/решение
A) 76
B) 79
C) 74
D) 77
E) 78
комментарий/решение
Задача №16. В комнате находятся 10 человек. Каждый из них либо рыцарь, который всегда говорит правду, либо лжец, который всегда лжет. Один из находящихся в комнате сказал: "В этой комнате $k_1$ лжецов", второй: "В этой комнате $k_2$ лжецов", $\ldots, 10$-ый: "В этой комнате $k_{10}$ лжецов". Известно, что все числа $k_1, k_2, \ldots, k_{10}$ не превосходят 10. Каково наибольшее возможное значение их суммы?
A) 100
B) 99
C) 98
D) 90
E) 94
комментарий/решение
A) 100
B) 99
C) 98
D) 90
E) 94
комментарий/решение
Задача №17. Вычислите сумму: $1 + 4 + 7 + \ldots + 2020 + 2023.$
A) 683100
B) 638100
C) 583100
D) 630100
E) 675100
комментарий/решение
A) 683100
B) 638100
C) 583100
D) 630100
E) 675100
комментарий/решение
Задача №18. Максат и его одноклассники стоят в кинотеатре рядом друг с другом в длинной очереди из 120 человек, чтобы купить билет на новый фильм. Максат — последний из одноклассников и 65-й в начале большой очереди. Однако Кайрат, одноклассник Максата, стоящий ближе всего к началу очереди, занимает 73-е место с конца большой очереди. Сколько одноклассников у Максата?
A) 17
B) 18
C) 16
D) 19
E) 20
комментарий/решение
A) 17
B) 18
C) 16
D) 19
E) 20
комментарий/решение
Задача №19. Сколько существует четырёхзначных чисел, у которых хотя бы одна цифра нечётная?
A) 8250
B) 8375
C) 8500
D) 9000
E) 9425
комментарий/решение
A) 8250
B) 8375
C) 8500
D) 9000
E) 9425
комментарий/решение
Задача №20. Кайрат хочет раскрасить клетки квадрата так, чтобы в каждой $3 \times 3$ строке, в каждом столбце и на обеих диагоналях было по три клетки трёх разных цветов. Каково наименьшее количество цветов потребуется Кайрату для такой раскраски?
A) 6
B) 4
C) 3
D) 5
E) 9
комментарий/решение
A) 6
B) 4
C) 3
D) 5
E) 9
комментарий/решение
Задача №21. Целые числа 3, 4, 5, 6, 12 и 13 (каждое число было использовано только один раз) написали в ряд на доске так, что сумма любых двух чисел, стоящих рядом, представляет собой полный квадрат. Найдите сумму средних двух чисел.
A) 9
B) 25
C) 16
D) 18
E) 22
комментарий/решение
A) 9
B) 25
C) 16
D) 18
E) 22
комментарий/решение
Задача №22. Произведение четырёх последовательных чётных натуральных чисел равно $2^8 \cdot 3^2 \cdot 5 \cdot 11$. Чему равна сумма этих четырёх чисел?
A) 84
B) 64
C) 68
D) 92
E) 76
комментарий/решение
A) 84
B) 64
C) 68
D) 92
E) 76
комментарий/решение
Задача №23. Сколько существует натуральных чисел меньше 1000, у которых сумма первой и последней цифр равна 13?
A) 60
B) 66
C) 57
D) 55
E) 63
комментарий/решение
A) 60
B) 66
C) 57
D) 55
E) 63
комментарий/решение
Задача №24. Экзамен по математике состоит из 20 задач. За правильный ответ студент получает 5 баллов, за неправильный ответ снимается 1 балл и за пустой ответ не начисляется ни одного балла. Инкар получает на экзамене 31 балл. Какое наибольшее количество задач она могла бы ответить (включая правильные и неправильные ответы)?
A) 16
B) 19
C) 17
D) 18
E) 20
комментарий/решение
A) 16
B) 19
C) 17
D) 18
E) 20
комментарий/решение
Задача №25. Абзал и Дарын работают на одной фабрике. После каждых девяти дней работы Абзал получает один выходной. После каждых шести дней работы Дарын получает один выходной. Сегодня выходной у Абзала, а завтра будет выходной у Дарына. Хотя бы через сколько дней с сегодняшнего дня у них будет один и тот же выходной?
A) 47
B) 56
C) 40
D) 50
E) 53
комментарий/решение
A) 47
B) 56
C) 40
D) 50
E) 53
комментарий/решение
Задача №26. Дана последовательность Фибоначчи: 1, 1, 2, 3, 5, 8, 13, 21, 34, $\ldots$ , то есть, каждое последующее число, начиная со второй, равно сумме двух предыдущих чисел. Найдите последнюю цифру числа стоящей на 2023-ем месте.
A) 7
B) 5
C) 3
D) 9
E) 8
комментарий/решение
A) 7
B) 5
C) 3
D) 9
E) 8
комментарий/решение
Задача №27. Три прямые, задаваемые уравнениями $ax+by=c$, $(a+2) x+(b-3) y=c+9$ и $(a+1) x+(b-1) y=c+2$ пересекаются в одной точке $M$. Чему равна сумма координат точки $M$?
A) $-8$
B) 0
C) $-2$
D) 6
E) 4
комментарий/решение
A) $-8$
B) 0
C) $-2$
D) 6
E) 4
комментарий/решение
Задача №28. Число звезд на небе равно $8 \times 12 + 98 \times 102 + 998 \times 1002 + \ldots + 99\ldots98 \times 100\ldots02$. В последнем члене цифра 9 встречается 2023 раз в 9 в $99\ldots 98$, а цифра 0 встречается 2023 раз в $100\ldots 02$. Какова сумма цифр количества звезд?
A) 2023
B) 2024
C) 2030
D) 2028
E) 2027
комментарий/решение
A) 2023
B) 2024
C) 2030
D) 2028
E) 2027
комментарий/решение
Задача №29. Выбрали четыре натуральных числа $x_1, x_2, x_3, x_4$ так, что $5\le x_1 \le x_2 \le x_3 \le x_4 \le 25$, при этом любые два из этих чисел отличаются друг от друга не меньше, чем на 5. Сколькими различными способами это можно сделать?
A) 84
B) 210
C) 126
D) 252
E) 148
комментарий/решение
A) 84
B) 210
C) 126
D) 252
E) 148
комментарий/решение
Задача №30. Положительные целые числа $m$ и $n$ таковы, что сумма и разность выражений $mn+m+n-53$ и $9n-6m+3$ являются простыми числами. Найдите произведение $mn$.
A) 72
B) 48
C) 63
D) 44
E) 54
комментарий/решение
A) 72
B) 48
C) 63
D) 44
E) 54
комментарий/решение