Европейская математическая олимпиада среди девочек (EGMO). 2023 год. Словения

Задача №1. Даны $n \geqslant 3$ действительных положительных чисел $a_{1}, a_{2}, \ldots, a_{n}$. Для каждого $1 \leqslant i \leqslant n$ пусть $b_{i}=\frac{a_{i-1}+a_{i+1}}{a_{i}}$ (здесь мы определяем $a_{0}$ как $a_{n}$, а также $a_{n+1}$ как $a_{1}$). Для всех $i$ и $j$ от 1 до $n$ включительно оказалось, что $a_{i} \leqslant a_{j}$ тогда и только тогда, когда $b_{i} \leqslant b_{j}$. Докажите, что $a_{1}=a_{2}=\cdots=a_{n}$.
комментарий/решение

Задача №2. Дан остроугольный треугольник $ABC$. Пусть $D$ — точка на его описанной окружности такая, что $AD$ — её диаметр. Точки $K$ и $L$ лежат на отрезках $AB$ и $AC$ соответственно так, что $DK$ и $DL$ — касательные к окружности, описанной около треугольника $AKL$. Докажите, что прямая $KL$ проходит через ортоцентр треугольника $ABC$.
Ортоцентром треугольника называется точка пересечения его высот.
комментарий/решение(1)

Задача №3. Пусть $k$ — целое положительное число. У Лекси есть словарь $\mathcal{D}$, состоящий из нескольких $k$-буквенных слов, содержащих только буквы $A$ и $B$. В каждую клетку таблицы $k \times k$ Лекси хочет вписать либо букву $A$, либо букву $B$ так, чтобы каждый столбец таблицы содержал слово из $\mathcal{D}$ при чтении сверху вниз, и каждая строка таблицы содержала слово из $\mathcal{D}$ при чтении слева направо.
Чему равно наименьшее целое число $m$ такое, что если $\mathcal{D}$ содержит не менее $m$ различных слов, то Лекси заведомо сможет заполнить таблицу нужным образом, независимо от того, какие слова находятся в $\mathcal{D}$?
комментарий/решение

Задача №4. Улитка Турбо сидит в некоторой точке окружности длиной 1. Дана бесконечная последовательность действительных положительных чисел $c_{1}, c_{2}, c_{3}, \ldots$. Турбо последовательно проползает расстояния $c_{1}, c_{2}, c_{3}, \ldots$ по этой окружности, каждый раз выбирая ползти ли ей по часовой стрелке или против часовой стрелки.
Например, если последовательность $c_{1}, c_{2}, c_{3}, \ldots$ это $0.4,0.6,0.3, \ldots$, то Турбо может начать ползти следующим образом:

Определите наибольшую константу $C > 0$ со следующим свойством: для любой последовательности действительных положительных чисел $c_{1}, c_{2}, c_{3}, \ldots$ таких, что $c_{i} < C$ для каждого $i$, Турбо может (после изучения последовательности) гарантировать, что на окружности есть точка, которую она никогда не посетит и не переползёт.
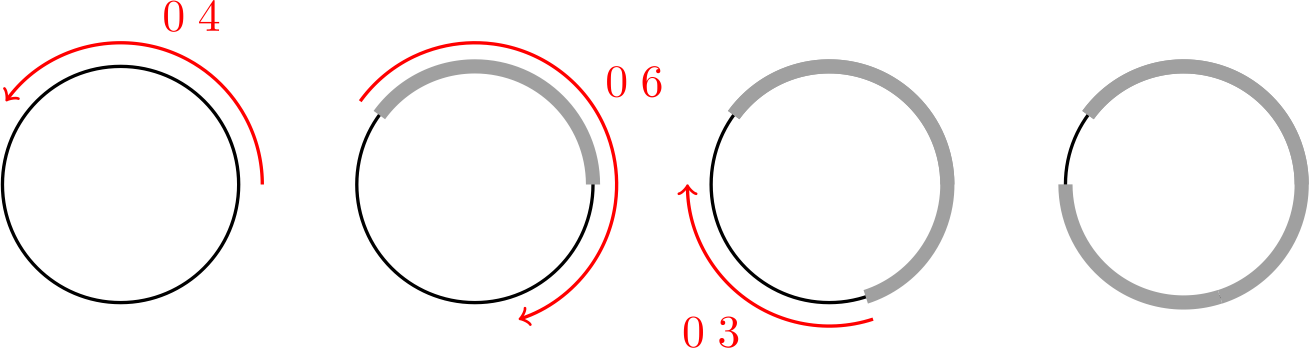
комментарий/решение

Задача №5. Дано целое положительное число $s \geqslant 2$. Для каждого целого положительного числа $k$ определим его реверсное значение $k'$ следующим образом: запишем $k$ в виде $a s+b$, где $a, b$ — целые неотрицательные числа и $b < s$, затем положим $k'=b s+a$. Для целого положительного числа $n$ рассмотрим бесконечную последовательность чисел $d_{1}, d_{2}, \ldots$, где $d_{1}=n$ и $d_{i+1}$ — реверсное значение числа $d_{i}$ для каждого целого положительного значения $i$.
Докажите, что эта последовательность содержит 1 тогда и только тогда, когда остаток при делении числа $n$ на число $s^{2}-1$ равен либо 1, либо $s$.
комментарий/решение

Задача №6. Дан треугольник $ABC$ с описанной около него окружностью $\Omega$. Пусть $S_{b}$ и $S_{c}$ — соответственно середины дуг $AC$ и $AB$, не содержащих третью вершину треугольника $ABC$. Пусть $N_{a}$ — середина дуги $BAC$ (дуги $BC$, содержащей вершину $A$). Пусть $I$ — центр вписанной окружности треугольника $ABC$. Пусть $\omega_{b}$ — окружность, которая касается прямой $AB$ и внутренним образом касается окружности $\Omega$ в точке $S_{b}$, и пусть $\omega_{c}$ — окружность, которая касается прямой $AC$ и внутренним образом касается окружности $\Omega$ в точке $S_{c}$. Докажите, что прямая $IN_{a}$ и прямая, проходящая через точки пересечения окружностей $\omega_{b}$ и $\omega_{c}$, пересекаются на окружности $\Omega$.
комментарий/решение

результаты