8-я олимпиада им. Шалтая Смагулова, 7 класс, 1 тур

Задача №1. В лесу в $\frac{1}{4}$ части обрезку прошли $40\%$ деревьев, а в оставшейся части — $20\%$. Какой процент всех деревьев в лесу прошли обрезку?
комментарий/решение

Задача №2. В треугольнике $ABC$ биссектрисы $AK$ и $BL$ пересекаются в точке $O$. Угол $AOB$ на 25 градусов больше угла $ALB$, и на 45 градусов больше угла $AKB$. Скольким градусам равен угол $ACB$?
комментарий/решение

Задача №3. Вычислите: $(4^8:8^4):(2^8:8^2):(2^4:4^2).$
комментарий/решение

Задача №4. Ученик выписал все такие натуральные числа, каждое из которых меньше любого числа, которое больше 2025, и больше любого числа, которое меньше 1952. Сколько чисел выписал ученик?
комментарий/решение

Задача №5. Найдите такое четырёхзначное число, что сумма его цифр без первой цифры равна 20, без второй цифры — 14, без третьей цифры — 17, без четвёртой — 12.
комментарий/решение(1)

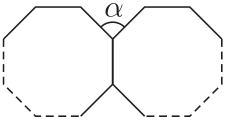
Задача №6. Соединив два одинаковых правильных $n$-угольника по стороне, получили угол $\alpha=40^\circ$ (см. рисунок). Найдите $n$.

комментарий/решение

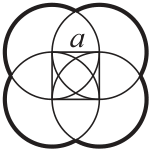
Задача №7. На рисунке центры четырёх окружностей лежат на вершинах квадрата со стороной $a=10$. Найдите длину криволинейной (жирной) фигуры. (В этой задаче считайте, что $\pi=3$.)

комментарий/решение

Задача №8. Пусть $n$ — наименьшее натуральное число, которое увеличивается в 9 раз при приписывании перед этим числом цифру 1. Найдите $n$.
комментарий/решение

Задача №9. В ряд выписали все делители четного натурального числа $n$ в порядке возрастания. Оказалось, что в этом ряду предпоследнее число на 615 больше второго числа. Найдите $n$.
комментарий/решение

Задача №10. Асан участвует на странной олимпиаде. Из 20 данных ему задач за каждую решенную из 10 легких задач ему дается 2 балла, а за каждую решенную из 10 сложных — дается 3 балла. За неправильно отвеченную легкую задачу снимается 3 балла, а за сложную снимается 2 балла. Самоуверенный Асан ответил на все задачи и получил 20 баллов. На сколько задач он ответил верно?
комментарий/решение

Задача №11. На рисунке дан заполненный магический квадрат $4\times 4$, заполненный натуральными числами от 1 до 16. Известно, что число 16 стоит в левом верхнем углу. Найдите сумму чисел в клетках, обозначенные звёздочкой. (Магический квадрат — это квадратная таблица заполненная числами так, что сумма чисел в каждой строке, в каждом столбце и на обеих главных диагоналях одинакова.)

комментарий/решение

Задача №12. Найдите наименьшее натуральное число, имеющее ровно 12 различных делителей, включая само число и 1.
комментарий/решение

Задача №13. Более $94\%$ детей в классе — мальчики. Какое наименьшее число детей может быть в этом классе? (В классе учится хотя бы одна девочка.)
комментарий/решение(1)

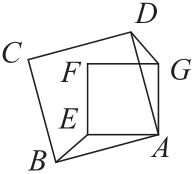
Задача №14. На рисунке периметр квадрата $ABCD$ равен 60, периметр квадрата $AEFG$ — 40, периметр треугольника $ABE$ — 31. Найдите длину отрезка $DG$.

комментарий/решение

Задача №15. Дан куб. Сколько существует равносторонних треугольников, вершины которых лежат в вершинах этого куба?
комментарий/решение

Задача №16. Дан равносторонний треугольник со $ABC$ стороной 24. Прямая пересекает отрезки $AB$, $BC$ и продолжение $AC$ в точках $D$, $E$ и $F$ соответственно (точка $C$ лежит на отрезке $AF$). Найдите длину отрезка $BD$, если $BD = CE = CF$.
комментарий/решение

Задача №17. Найдите произведение двух наибольших целых решений системы неравенств: $x^3\le 729 \le x^2$.
комментарий/решение

Задача №18. Найдите натуральное число $n$, если $1+2+\ldots+(n-1)+n+(n-1)+\ldots+2+1=676.$
комментарий/решение(1)

Задача №19. Пусть $A=\frac{4}{1\cdot 3}-\frac{8}{3\cdot 5}+\frac{12}{5\cdot 7}-\frac{16}{7\cdot 9}+\frac{20}{9\cdot 11}-\ldots-\frac{2024}{1011\cdot 1013}.$ Найдите значение выражения $1013\cdot A$.
комментарий/решение(1)

Задача №20. Арман привёл произведение $1\cdot 7\cdot 13\cdot 19\cdot 25\cdot \ldots\cdot 2023$ в вид $5^x \cdot 7^y \cdot z$, здесь $x$, $y$, $z$ — натуральные числа, а $z$ не делится ни на 5, ни на 7. Найдите сумму $x+y$.
комментарий/решение