Областная олимпиада по математике, 2003 год, 10 класс
Комментарий/решение:
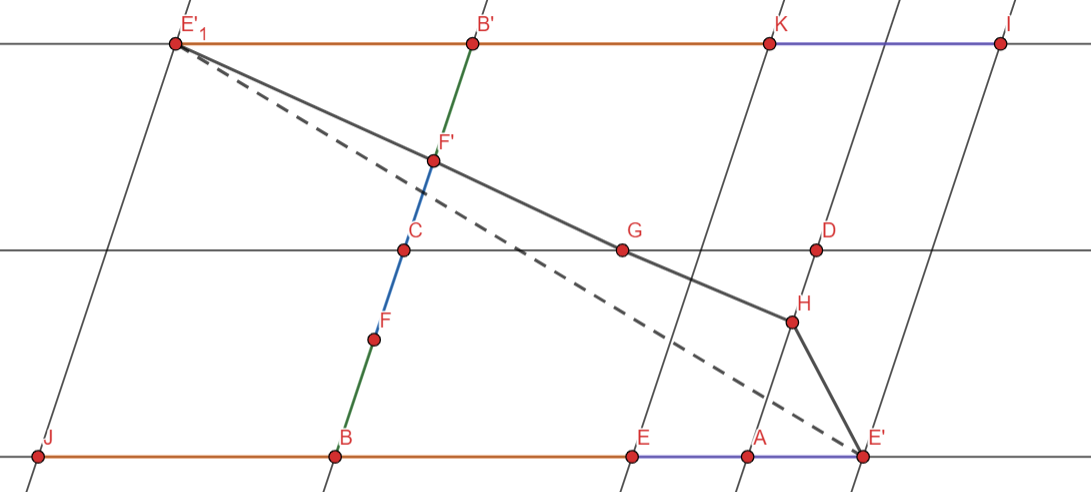
Пусть в параллелограмме $ABCD$ диагональ $AC$ меньшая, тогда $\angle DAB \geq 90, \angle BCD \geq 90$. На сторонах $AB,BC,CD,DA$ возьмем точки $E,F,G,H$ соответственно. Пусть $E'$ и $F'$ - точки симметричные $E$ и $F$ относительно $A$ и $C$ соответственно. Тогда $\angle HAE' \leq 90, \angle GCF' \leq 90$, следовательно $E'H \leq EH, F'G \leq FG$. Пусть $E'_1, B'$ - точки симметричные $E$ и $B$ относительно $C$. тогда $E'_1B'=EB$, $FB=F'B'$, $\angle FBE=\angle F'B'E'_1$, то есть $EF=E"_1F'$. Пусть $I$ на прямой $E'_1B'$ такая, что $E'I||BC$, $J$ на прямой $AB$ такая, что $JE'_1||BC$. Тогда $IE'_1JE'$ - параллелограмм, в котором $E'J=2*AB$, $E'I=2*AD$, значит $E'E'_1=2*AC$. Получаем, что $EF+FG+GH+HE \geq E'H+HG+GF'+F'E'_1 \geq E'E'_1=2*AC$.
Возможно, что при неправильном наборе формул, они будут
доредактированы модератором. При этом содержание не будет меняться.