6-я Жаутыковская олимпиада (2010), теоретический тур
Опыт Толмена и Стюарта (10 баллов)
В 1916 году Толмен и Стюарт поставили знаменитый опыт, подтверждающий, что ток в металлах обусловлен движением свободных электронов. Схема опыта изображена на рисунке слева.
Очень длинная катушка имеет собственный момент инерции $J_0$, радиус $r$ и длину $h$. На катушку намотан один слой тонкого металлического провода, имеющего длину $l$, массу $m$, число витков на единицу длины равно $n$. Концы провода с помощью скользящих контактов замкнуты на гальванометр. Катушка с проводом приводится в быстрое вращение с угловой скоростью $\omega_0$, а затем останавливается трением с моментом силы $M$. Полное сопротивление цепи равно $R$, а ее емкостью можно пренебречь.
Часть 1. В этой части полностью пренебрегается индуктивностью катушки и предполагается выполнение закона Ома в любой момент времени. Дайте ответы на следующие вопросы:
посмотреть в олимпиаде
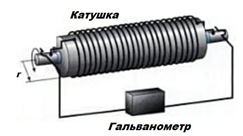
В 1916 году Толмен и Стюарт поставили знаменитый опыт, подтверждающий, что ток в металлах обусловлен движением свободных электронов. Схема опыта изображена на рисунке слева.
Очень длинная катушка имеет собственный момент инерции $J_0$, радиус $r$ и длину $h$. На катушку намотан один слой тонкого металлического провода, имеющего длину $l$, массу $m$, число витков на единицу длины равно $n$. Концы провода с помощью скользящих контактов замкнуты на гальванометр. Катушка с проводом приводится в быстрое вращение с угловой скоростью $\omega_0$, а затем останавливается трением с моментом силы $M$. Полное сопротивление цепи равно $R$, а ее емкостью можно пренебречь.
Часть 1. В этой части полностью пренебрегается индуктивностью катушки и предполагается выполнение закона Ома в любой момент времени. Дайте ответы на следующие вопросы:
- [1 балл] Определите полный момент инерции $J$ катушки с проводом. Ответ выразите через $J_0$, $M$, $\omega_0$.
- [1 балл] Определите зависимость угловой скорости вращения катушки $\omega(t)$ от времени $t$. Ответ выразите через $J$, $M$, $\omega_0$.
- [1 балл] Определите зависимость силы тока в цепи катушки $I(t)$ от времени $t$. Ответ выразите через $J$, $M$, $r$, $l$, $R$ и $m_{e}$, $e$ — массу и заряд электрона, соответственно.
- [2 балла] Гальванометр зафиксировал протекший через него электрический заряд $Q$. Выразите отношение заряда электрона к его массе $e/m_{e}$ через $\omega_0$, $r$, $l$, $R$, $Q$.
- [1 балл] Найдите максимальное значение тока $I_{\max}$ в катушке. Ответ выразите через $J$, $M$, $r$, $l$, $R$ и $m_{e}$, $e$. Изобразите примерный график зависимости $I(t)$.
- [1 балл] Найдите максимальную энергию $W_0$, запасенную в катушке. Ответ выразите через $J$, $M$, $r$, $l$, $R$ и $m_{e}$, $e$, $n$, $h$ и магнитную постоянную $\mu_0$.
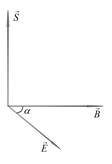
- [3 балла] Поток $S$ электромагнитной энергии через единицу площади поверхности определяется вектором Пойнтинга, который перпендикулярен электрическому и магнитному полю и равен по модулю $S=\frac{1}{\mu_{0}}EB \sin\alpha$, где $E$ — вектор напряженности электрического поля, $B$ — вектор магнитной индукции, а $\alpha$ — угол между ними (смотрите рисунок справа). Определите электромагнитную энергию $W$, проходящую через боковую поверхность катушки за время нарастания тока, и электромагнитную энергию $W'$, проходящую через боковую поверхность за время убывания тока. Ответ выразите через $l$, $r$, $M$, $J$, $n$, $R$, $m_{e}$, $e$, $\mu_0$.
Часть 2. В этой части необходимо учесть малую индуктивность катушки, которая считается очень длинной, так что краевыми эффектами можно пренебречь. Дайте ответы на следующие вопросы:
Комментарий/решение:
Возможно, что при неправильном наборе формул, они будут
доредактированы модератором. При этом содержание не будет меняться.