6-я Жаутыковская олимпиада (2010), теоретический тур

Эта задача состоит из трех частей, не связанных друг с другом.
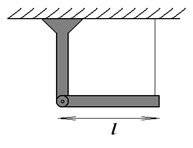
1А (3 балла) Один конец однородного твердого стержня массой $m$ и длиной $l$ подвешен к вертикальной опоре с помощью идеального шарнира, а второй подвешен на нити, так что стержень находится в горизонтальном положении. В некоторый момент времени нить перерезают. Найти силу реакции опоры в шарнире в зависимости от угла отклонения стержня от горизонтального положения.

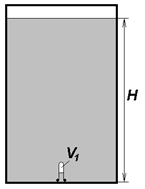
1В (4 балла) Плотность слоя жидкости высотой $H$, заполняющей полностью закрытый толстостенный цилиндрический сосуд, линейно уменьшается с высотой от $\rho_{\max}$ до малой величины, которую можно принять равной нулю. Над жидкостью находится тонкий слой насыщенного пара, давлением которого можно пренебречь по сравнению с гидростатическим давлением жидкости. Снизу в жидкость погружают перевернутую пробирку объемом $V_0$, масса $M$ которой сосредоточена возле горлышка, а длина значительно меньше $H$. В пробирке находится газ, занимающий объем $V_1$, масса которого значительно меньше массы пробирки. Температура системы поддерживается постоянной. Может ли пробирка неподвижно зависнуть в сосуде? Если да, то при каких условиях и на какой высоте от дна? Будет ли ее положение равновесия устойчивым? Объем стенок пробирки мал по сравнению с $V_1$.

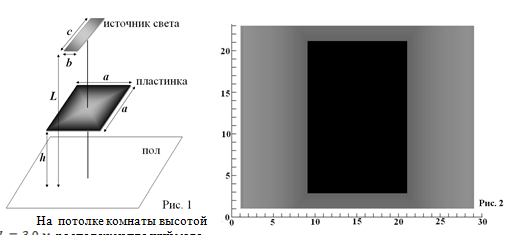
1C (3 балла) На потолке комнаты высотой $L=3$м расположен плоский матовый светильник, имеющий форму прямоугольника размерами $c\times b$. Под светильником на высоте $h$ над полом горизонтально расположили непрозрачную квадратную пластинку со стороной $a=10$см (см. рис.1). На рис.2 схематически изображен вид тени, отбрасываемой пластинкой на пол комнаты: тень состоит из темного прямоугольника, окруженного другим более светлым прямоугольником, причем при приближении к краям этого внешнего прямоугольника тень светлеет. Цена деления шкал на этом рисунке 1,0 см. Определите размеры источника света $b$ и $c$, и высоту $h$ над полом, на которой расположена пластинка. Укажите ориентацию источника света по отношению к тени, отбрасываемой пластинкой.