13-я Жаутыковская олимпиада (2017), теоретический тур
(10,0 балла)
Сопротивление призмы
1. Математическое введение (3,0 балла) По определению считается, что члены числовой последовательности $x_0,x_1,x_2,...$ подчиняются рекуррентному соотношению, если каждый последующий из них выражается через предыдущие. Например, для известной вам геометрической прогрессии $$x_{k}=\lambda x_{k-1},\quad (1)$$ где $k=1,2,3,...,\lambda$, $\lambda$ — некоторое фиксированное число, а нулевой член последовательности имеет некоторое значение $A$, то есть $x_0=A$.
1.1 [0,2 балла] Получите формулу для произвольного члена последовательности $x_{k}$ в явном виде, т.е. выразите его через номер $k$, начальное значение $A$ и $\lambda$.
Теперь рассмотрим число $\lambda=2+\sqrt{3}$. При возведении в целую натуральную степень $k$, его можно представить в виде $$\lambda^{k}=p_{k}+q_{k}\sqrt{3},\quad (2)$$ где $p_{k}$, $q_{k}$ — некоторые целые числа.
1.2 [0,4 балла] Запишите рекуррентные соотношения, выражающие значения $p_{k}$, $q_{k}$ через предыдущие значения $p_{k-1}$, $q_{k-1}$. Запишите также обратные соотношения, выражающие $p_{k-1}$, $q_{k-1}$ через $p_{k}$, $q_{k}$.
1.3 [0,7 балла] Рассчитайте численные значения коэффициентов $p_{k}$, $q_{k}$ для $k=1,2,3,4,5$.
1.4 [0,2 балла] Выразите число $\lambda^{-k}=(2+\sqrt3)^{-k}$ через найденные величины $p_{k}$, $q_{k}$.
Пусть члены некоторой числовой последовательности подчиняются рекуррентному соотношению $$x_{k+1}=4x_{k}-x_{k-1},\hspace{5px} k=1,...,N-1,\eqno(3)$$ причем известно, что $N$ — некоторое целое число, а $x_0=A$ и $x_{N}=B$, $A$, $B$ — произвольные числа.
1.5 [1,0 балла] Получите формулу для произвольного члена $x_{k}$ последовательности $(3)$ в явном виде, т.е. выразите его через номер $k$ и величины $A$, $B$, $N$.
1.6 [0,5 балла] Выразите произвольный член последовательности $x_{k}$ через величины $p_{k}$, $q_{k}$, найденные в пп.1.2-1.3.
Подсказка. Решение рекуррентного соотношения $(3)$ нужно искать в виде $x_{k}=C\lambda^{k}$, где $C$ — некоторая константа. Найдите, при каких значениях $\lambda$ это возможно и постройте общее решение, удовлетворяющее заданным условиям.
2. Проволочный каркас в форме призмы (7,0 балла)
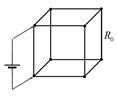
Широко известны задачи, в которых требуется найти электрическое сопротивление простейших проволочных каркасов. Пример одного из таких каркасов в форме куба показан на рисунке внизу. Пусть электрическое сопротивление каждого ребра равно $R_0$.
2.1 [0,8 балла] Найдите сопротивление куба при подключении источника к вершинам одного ребра, как показано на рисунке справа.
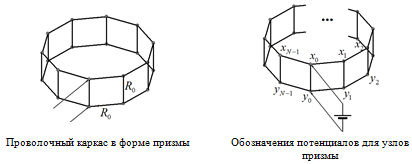
Давайте рассмотрим более общий случай проволочного каркаса в форме правильной призмы с произвольным числом боковых граней $N$ и определим его электрическое сопротивление при подключении источника к вершинам одного из боковых ребер, как показано на рисунке внизу. Сопротивление каждого ребра каркаса равно $R_0$.
Для удобства пронумеруем вершины призмы и обозначим их электрические потенциалы: на верхней грани $x_{k}$, а на нижней грани $y_{k}$, как показано на рисунке внизу. Источник постоянного напряжения подключен к вершинам нулевого ребра. Будем считать, что источник задает потенциалы вершин ребра равными $x_0=+\varphi_0$ и $y_0=-\varphi_0$ соответственно.
2.2 [0,2 балла] Запишите соотношение, которое связывает значения потенциалов $x_{k}$ и $y_{k}$. Запишите соотношение, которое связывает значения потенциалов $x_{k}$ и $x_{N-k}$.
Рассмотрим произвольное боковое ребро призмы, кроме нулевого $k=0$ и последнего $k=N-1$. Соответствующая электрическая схема показана на рисунке ниже.
2.3 [1,0 балла] Запишите соотношение, связывающие значения потенциала $x_{k}$ со значениями потенциалов в соседних вершинах для $k=1,2,...,N-2$.
2.4 [0,2 балла] Запишите граничные условия в точках $k=0$ и $k=N-1$, позволяющие определить значения потенциалов $x_{k}$ однозначно.
2.5 [0,2 балла] Найдите явные выражения для потенциалов $x_{k}$ и $y_{k}$ для всех значений $k=0,1,2,...,N-1$.
2.6 [0,4 балла] Выразите значение силы тока, протекающего через источник, через величины $\varphi_0$, $R_0$, $N$. Используйте найденные в Математическом введении числа $p_{k}$, $q_{k}$.
2.7 [0,2 балла] Получите явную формулу для сопротивления проволочного каркаса $R_{N}$, выразив его через величины $R_0$, $p_{N}$, $q_{N}$.
2.8 [1,0 балла] Рассчитайте точные значения сопротивлений каркаса для $N=1,2,3,4,5$.
2.9 [0,5 балла] Нарисуйте эквивалентные электрические схемы для «экзотических» призм с $N=1$ и $N=2$.
2.10 [1,0 балла] Найдите значения сопротивления $R_{\infty}$ каркаса при $N\to \infty$.
2.11 [1,5 балла] Найдите минимальное значение $N$, при котором сопротивление призмы отличается от $R_{\infty}$ не более чем на $2\%$.
посмотреть в олимпиаде
1. Математическое введение (3,0 балла) По определению считается, что члены числовой последовательности $x_0,x_1,x_2,...$ подчиняются рекуррентному соотношению, если каждый последующий из них выражается через предыдущие. Например, для известной вам геометрической прогрессии $$x_{k}=\lambda x_{k-1},\quad (1)$$ где $k=1,2,3,...,\lambda$, $\lambda$ — некоторое фиксированное число, а нулевой член последовательности имеет некоторое значение $A$, то есть $x_0=A$.
1.1 [0,2 балла] Получите формулу для произвольного члена последовательности $x_{k}$ в явном виде, т.е. выразите его через номер $k$, начальное значение $A$ и $\lambda$.
Теперь рассмотрим число $\lambda=2+\sqrt{3}$. При возведении в целую натуральную степень $k$, его можно представить в виде $$\lambda^{k}=p_{k}+q_{k}\sqrt{3},\quad (2)$$ где $p_{k}$, $q_{k}$ — некоторые целые числа.
1.2 [0,4 балла] Запишите рекуррентные соотношения, выражающие значения $p_{k}$, $q_{k}$ через предыдущие значения $p_{k-1}$, $q_{k-1}$. Запишите также обратные соотношения, выражающие $p_{k-1}$, $q_{k-1}$ через $p_{k}$, $q_{k}$.
1.3 [0,7 балла] Рассчитайте численные значения коэффициентов $p_{k}$, $q_{k}$ для $k=1,2,3,4,5$.
1.4 [0,2 балла] Выразите число $\lambda^{-k}=(2+\sqrt3)^{-k}$ через найденные величины $p_{k}$, $q_{k}$.
Пусть члены некоторой числовой последовательности подчиняются рекуррентному соотношению $$x_{k+1}=4x_{k}-x_{k-1},\hspace{5px} k=1,...,N-1,\eqno(3)$$ причем известно, что $N$ — некоторое целое число, а $x_0=A$ и $x_{N}=B$, $A$, $B$ — произвольные числа.
1.5 [1,0 балла] Получите формулу для произвольного члена $x_{k}$ последовательности $(3)$ в явном виде, т.е. выразите его через номер $k$ и величины $A$, $B$, $N$.
1.6 [0,5 балла] Выразите произвольный член последовательности $x_{k}$ через величины $p_{k}$, $q_{k}$, найденные в пп.1.2-1.3.
Подсказка. Решение рекуррентного соотношения $(3)$ нужно искать в виде $x_{k}=C\lambda^{k}$, где $C$ — некоторая константа. Найдите, при каких значениях $\lambda$ это возможно и постройте общее решение, удовлетворяющее заданным условиям.
2. Проволочный каркас в форме призмы (7,0 балла)
Широко известны задачи, в которых требуется найти электрическое сопротивление простейших проволочных каркасов. Пример одного из таких каркасов в форме куба показан на рисунке внизу. Пусть электрическое сопротивление каждого ребра равно $R_0$.
2.1 [0,8 балла] Найдите сопротивление куба при подключении источника к вершинам одного ребра, как показано на рисунке справа.
Давайте рассмотрим более общий случай проволочного каркаса в форме правильной призмы с произвольным числом боковых граней $N$ и определим его электрическое сопротивление при подключении источника к вершинам одного из боковых ребер, как показано на рисунке внизу. Сопротивление каждого ребра каркаса равно $R_0$.
Для удобства пронумеруем вершины призмы и обозначим их электрические потенциалы: на верхней грани $x_{k}$, а на нижней грани $y_{k}$, как показано на рисунке внизу. Источник постоянного напряжения подключен к вершинам нулевого ребра. Будем считать, что источник задает потенциалы вершин ребра равными $x_0=+\varphi_0$ и $y_0=-\varphi_0$ соответственно.
2.2 [0,2 балла] Запишите соотношение, которое связывает значения потенциалов $x_{k}$ и $y_{k}$. Запишите соотношение, которое связывает значения потенциалов $x_{k}$ и $x_{N-k}$.
Рассмотрим произвольное боковое ребро призмы, кроме нулевого $k=0$ и последнего $k=N-1$. Соответствующая электрическая схема показана на рисунке ниже.
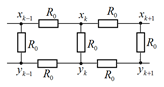
2.3 [1,0 балла] Запишите соотношение, связывающие значения потенциала $x_{k}$ со значениями потенциалов в соседних вершинах для $k=1,2,...,N-2$.
2.4 [0,2 балла] Запишите граничные условия в точках $k=0$ и $k=N-1$, позволяющие определить значения потенциалов $x_{k}$ однозначно.
2.5 [0,2 балла] Найдите явные выражения для потенциалов $x_{k}$ и $y_{k}$ для всех значений $k=0,1,2,...,N-1$.
2.6 [0,4 балла] Выразите значение силы тока, протекающего через источник, через величины $\varphi_0$, $R_0$, $N$. Используйте найденные в Математическом введении числа $p_{k}$, $q_{k}$.
2.7 [0,2 балла] Получите явную формулу для сопротивления проволочного каркаса $R_{N}$, выразив его через величины $R_0$, $p_{N}$, $q_{N}$.
2.8 [1,0 балла] Рассчитайте точные значения сопротивлений каркаса для $N=1,2,3,4,5$.
2.9 [0,5 балла] Нарисуйте эквивалентные электрические схемы для «экзотических» призм с $N=1$ и $N=2$.
2.10 [1,0 балла] Найдите значения сопротивления $R_{\infty}$ каркаса при $N\to \infty$.
2.11 [1,5 балла] Найдите минимальное значение $N$, при котором сопротивление призмы отличается от $R_{\infty}$ не более чем на $2\%$.
Комментарий/решение:
Возможно, что при неправильном наборе формул, они будут
доредактированы модератором. При этом содержание не будет меняться.