12-я Жаутыковская олимпиада (2016), теоретический тур
(10,0 балла)
Эта задача состоит из трех частей, не связанных друг с другом.
Задача 1А (4.0 балла) Однородная планета радиуса $R$ не имеет атмосферы и не вращается. С поверхности планеты бросают камень под углом $\alpha$ к горизонту со скоростью $\vartheta_0$, равной первой космической скорости на поверхности этой планеты. Найдите максимальную высоту подъёма камня над поверхностью планеты. На каком расстоянии от места броска, измеренном вдоль поверхности, камень упадёт?
Задача 1В (3.0 балла)
Задача 1С (3.0 балла)
посмотреть в олимпиаде
Комментарий/решение:
Задача 1А (4.0 балла) Однородная планета радиуса $R$ не имеет атмосферы и не вращается. С поверхности планеты бросают камень под углом $\alpha$ к горизонту со скоростью $\vartheta_0$, равной первой космической скорости на поверхности этой планеты. Найдите максимальную высоту подъёма камня над поверхностью планеты. На каком расстоянии от места броска, измеренном вдоль поверхности, камень упадёт?
Задача 1В (3.0 балла)
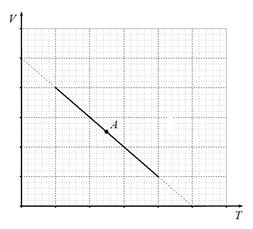
Задача 1С (3.0 балла)
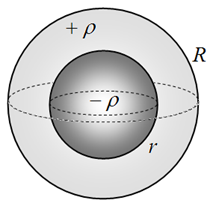
Комментарий/решение:
Возможно, что при неправильном наборе формул, они будут
доредактированы модератором. При этом содержание не будет меняться.