9-я Жаутыковская олимпиада (2013), теоретический тур

(10 баллов)
Эта задача состоит из трех частей, не связанных друг с другом. Задача 1.А Блок (5.0 балла) На круглый блок радиуса $R$ положили канат длиной $L$ и массы $m$, который начал соскальзывать с блока без трения. В момент, когда разность высот свисающих с блока концов каната равна половине длины каната, найти:
1. ускорение каната;
2. натяжение каната в верхней точке;
3. точку каната, в которой сила натяжения максимальна (достаточно найти угол между радиусом в эту точку и вертикалью).
Задача 1.В. Запарь (2.0 балла) В физической лаборатории термометр показывал $20^{\circ}$ C, а барометр — $1$ атм. Лаборант Запарь достал из шкафа прочный сосуд, налил в него немного воды и герметично закрыл крышкой. Затем Запарь медленно нагрел сосуд до $200^{\circ}$ C. При этой температуре давление в сосуде составило $2,88$ атм. Определите температуру, при которой вся вода испарилась.
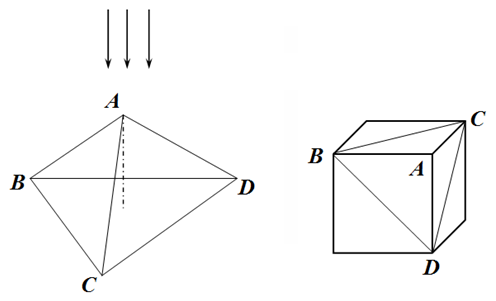
Задача 1.С. Пирамида (3.0 балла) Правильная треугольная пирамида $ABCD$ изготовлена из прозрачного материала с показателем преломления $n=1,6$. Все углы при вершине пирамиды $A$ — прямые. В основании пирамиды лежит правильный треугольник $BCD$, длины сторон которого равны $a=2$ мм. Эту пирамиду также можно представить, как «угол, отрезанный от куба». Пирамида однородно освещается так, что свет падает вдоль ее высоты, перпендикулярно плоскости основания.
1. Нарисуйте, область на основании пирамиды, освещенную светом, преломленным гранью $ABC$;

2. Параллельно основанию пирамиды на расстоянии $L=10$ см от него расположен экран. Нарисуйте области освещенные светом, преломленным пирамидой, на этом экране. Укажите положение и размеры этих областей.