8-я Жаутыковская олимпиада (2012), теоретический тур
(10 баллов)
Ядерная капля. В этой задаче рассматриваются основные характеристики и условия устойчивости атомных ядер. Пусть атомное ядро содержит $A$ нуклонов ($A$ — атомный вес элемента), а именно $Z$ протонов ($Z$ — порядковый номер в таблице элементов) и $N=A-Z$ нейтронов. При этом выражение для полной энергии ядра записывается в виде $$E=\left(Zm_{p}+Nm_{n}\right)c^2+E_{p}(A,Z)=Mc^2,\quad (1)$$ где $M$ — масса ядра, $m_{p}$ — масса свободного протона, $m_{n}$ — масса свободного нейтрона, $C$ — скорость света, а $e_{P}$ — потенциальная энергия взаимодействия нуклонов в ядре. Потенциальная энергия взаимодействия нуклонов может быть описана следующей полуэмпирической формулой Вайцзеккера $$E_{p}(A,Z)=-a_1A+a_2A^{2/3}+a_3\frac{Z^2}{A^{1/3}}+a_4\frac{(A/2-Z)^2}{A},\quad (2)$$ где $a_1=15,8$ МэВ, $a_2=16,8$ МэВ, $a_3=0,72$ МэВ, $a_4=23,5$ МэВ. Полуэмпирическая формула Вайцзеккера соответствует одной из простейших моде-лей атомного ядра, так называемой модели сферической жидкой капли, которая основывается на аналогии между ядром и каплей обычной жидкости. При этом масса и заряд ядра считаются равномерно распределенными внутри шара некоторого радиуса, а сама нуклонная жидкость характеризуется некоторым параметром $\sigma$, являющимся аналогом коэффициента поверхностного натяжения жидкости.
В формуле для потенциальной энергии $E_{p}$ учитывались следующие вклады:
3.1 [2 балла] Найдите электростатическую энергию $E_{C}$ шара радиуса $R$, равномерно заряженного по объёму зарядом $Q$. Ответ выразите через заряд $Q$, диэлектрическую постоянную $\epsilon_0$ и радиус шара $R$;
3.2 [1 балл] Найдите формулу и численное значение коэффициента $R_0$ в формуле $(3)$;
3.3 [1 балл] Найдите формулу и численное значение плотности ядерного вещества $\rho_{m}$;
3.4 [1 балл] Найдите формулу и численное значение коэффициента поверхностного натяжения $\sigma$ нуклонной жидкости. Допустим теперь, что ядро делится на две части с атомными весами $kA$ и $(1-k)A$, где $0 3.5 [2 балла] Деление ядра становится энергетически выгодным при выполнении условия $Z^2/A>f(k)$. Найдите выражение для функции $f(k)$ и постройте ее схематический график.
3.6 [0.5 балла] Найдите предельное значение $(Z^2/A)_0$, при котором самопроизвольное деление еще теоретически возможно. При выполнении условия из п. $3.5$ ядро может существовать достаточно долго. Например, период полураспада ядра урана-$235$ равен $713$ миллионов лет. Следовательно, мгновенному делению ядер препятствует некоторый энергетический барьер, который исчезает при некотором критическом значении $(Z^2/A)_{\text{\text{critical}}}$. В действительности, ядро начнет делиться только при значительном отклонении его формы от сферической.
3.7 [0.5 балла] Найдите соотношение между $\epsilon$ и $\lambda$. Расчеты показывают, что энергия электростатического взаимодействия протонов деформированного ядра составляет приблизительно $E_{C}^{\text{deformed}}=E_{C}\left(l-\frac{1}{6}\epsilon (\epsilon+\lambda)\right)$.
3.8 [2 балла] Получите выражение и найдите численное значение $(Z^2/A)_{\text{critical}}$. Известны следующие физические константы: Элементарный заряд $e=1,609\times10^{-19}$ Кл
Диэлектрическая постоянная $\epsilon_0=8,85\times10^{-12}$ Ф/м Масса нуклона (протона или нейтрона) $m_{p}\thickapprox m_{n}\thickapprox m=1,67\times 10^{-27}$ кг $1$ еВ $=e\times 1$ В $=1,609\times 10^{-19}$ Дж При решении данных задач вы можете использовать формулы: $$arc\sin(x)\thickapprox x+\frac{x^3}{6}, при |x|\ll 1$$ $$(1+x)^{\alpha}\thickapprox 1+\alpha x +\frac{\alpha(\alpha-1)}{2}x^2, при |x|\ll 1$$
посмотреть в олимпиаде
Ядерная капля. В этой задаче рассматриваются основные характеристики и условия устойчивости атомных ядер. Пусть атомное ядро содержит $A$ нуклонов ($A$ — атомный вес элемента), а именно $Z$ протонов ($Z$ — порядковый номер в таблице элементов) и $N=A-Z$ нейтронов. При этом выражение для полной энергии ядра записывается в виде $$E=\left(Zm_{p}+Nm_{n}\right)c^2+E_{p}(A,Z)=Mc^2,\quad (1)$$ где $M$ — масса ядра, $m_{p}$ — масса свободного протона, $m_{n}$ — масса свободного нейтрона, $C$ — скорость света, а $e_{P}$ — потенциальная энергия взаимодействия нуклонов в ядре. Потенциальная энергия взаимодействия нуклонов может быть описана следующей полуэмпирической формулой Вайцзеккера $$E_{p}(A,Z)=-a_1A+a_2A^{2/3}+a_3\frac{Z^2}{A^{1/3}}+a_4\frac{(A/2-Z)^2}{A},\quad (2)$$ где $a_1=15,8$ МэВ, $a_2=16,8$ МэВ, $a_3=0,72$ МэВ, $a_4=23,5$ МэВ. Полуэмпирическая формула Вайцзеккера соответствует одной из простейших моде-лей атомного ядра, так называемой модели сферической жидкой капли, которая основывается на аналогии между ядром и каплей обычной жидкости. При этом масса и заряд ядра считаются равномерно распределенными внутри шара некоторого радиуса, а сама нуклонная жидкость характеризуется некоторым параметром $\sigma$, являющимся аналогом коэффициента поверхностного натяжения жидкости.
В формуле для потенциальной энергии $E_{p}$ учитывались следующие вклады:
- поверхностная энергия, учитывающая поверхностное натяжение ядерной материи в модели жидкой капли;
- энергию кулоновского отталкивания протонов, входящих в ядро;
- обменная энергия взаимодействия, отражающая тенденцию к стабильности ядер с $N=Z$;
- прямая зависимость от числа нуклонов $A$ вследствие действия ядерных сил. Также в выводе этой полуэмпирической формулы Вайцзеккер использовал экспериментально установленную зависимость радиуса атомного ядра от числа нуклонов
3.1 [2 балла] Найдите электростатическую энергию $E_{C}$ шара радиуса $R$, равномерно заряженного по объёму зарядом $Q$. Ответ выразите через заряд $Q$, диэлектрическую постоянную $\epsilon_0$ и радиус шара $R$;
3.2 [1 балл] Найдите формулу и численное значение коэффициента $R_0$ в формуле $(3)$;
3.3 [1 балл] Найдите формулу и численное значение плотности ядерного вещества $\rho_{m}$;
3.4 [1 балл] Найдите формулу и численное значение коэффициента поверхностного натяжения $\sigma$ нуклонной жидкости. Допустим теперь, что ядро делится на две части с атомными весами $kA$ и $(1-k)A$, где $0
3.6 [0.5 балла] Найдите предельное значение $(Z^2/A)_0$, при котором самопроизвольное деление еще теоретически возможно. При выполнении условия из п. $3.5$ ядро может существовать достаточно долго. Например, период полураспада ядра урана-$235$ равен $713$ миллионов лет. Следовательно, мгновенному делению ядер препятствует некоторый энергетический барьер, который исчезает при некотором критическом значении $(Z^2/A)_{\text{\text{critical}}}$. В действительности, ядро начнет делиться только при значительном отклонении его формы от сферической.
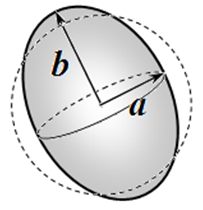
3.7 [0.5 балла] Найдите соотношение между $\epsilon$ и $\lambda$. Расчеты показывают, что энергия электростатического взаимодействия протонов деформированного ядра составляет приблизительно $E_{C}^{\text{deformed}}=E_{C}\left(l-\frac{1}{6}\epsilon (\epsilon+\lambda)\right)$.
3.8 [2 балла] Получите выражение и найдите численное значение $(Z^2/A)_{\text{critical}}$. Известны следующие физические константы: Элементарный заряд $e=1,609\times10^{-19}$ Кл
Диэлектрическая постоянная $\epsilon_0=8,85\times10^{-12}$ Ф/м Масса нуклона (протона или нейтрона) $m_{p}\thickapprox m_{n}\thickapprox m=1,67\times 10^{-27}$ кг $1$ еВ $=e\times 1$ В $=1,609\times 10^{-19}$ Дж При решении данных задач вы можете использовать формулы: $$arc\sin(x)\thickapprox x+\frac{x^3}{6}, при |x|\ll 1$$ $$(1+x)^{\alpha}\thickapprox 1+\alpha x +\frac{\alpha(\alpha-1)}{2}x^2, при |x|\ll 1$$
Комментарий/решение:
Возможно, что при неправильном наборе формул, они будут
доредактированы модератором. При этом содержание не будет меняться.