7-я Жаутыковская олимпиада (2011), экспериментальный тур

Деформация, гистерезис, бистабильность

Приборы и принадлежности: резиновый шнур, подставка деревянная, линейка деревянная, набор грузов $6\times 100$ г, мерная лента, нитки, кнопки канцелярские. Рис. 1
Часть 1. Растяжение. (4,5 балла)

1.1.Подвесьте резиновый шнур на боковом торце подставки с помощью кнопки (рис.1). Измерьте зависимость длины шнура $L$ от силы тяжести подвешенных грузов. Измерения проведите в двух «направлениях»: при нагрузке — последовательно увеличивая число грузов от $0$ до $6$;при разгрузке — последовательно уменьшая число грузов от $6$ до нуля
1.2. Постройте на одном рисунке графики зависимости относительного удлинения шнура от приложенной к нему силы тяжести грузов при нагрузке и разгрузке.
Часть 2. Равновесие. (7,5 балла)

Расположите линейку возле вертикальной стенки подставки, как показано на рис. 2. К верхней части линейки прикрепите с помощью кнопок резиновый шнур. Второй конец шнура закрепите на подставке также с помощью кнопок. Длина шнура $l_0$ в недеформированном состоянии должна составлять примерно $8$ см. Расстояние от нижнего упора до верхнего края вертикальной стенки подставки равно длине линейки. Прикрепите к верхней части линейки нитку, к которой можно подвешивать грузы.
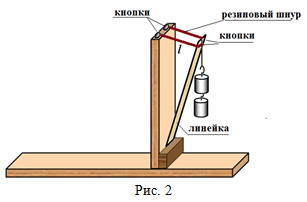
Внимание! Вам необходимо будет измерить длину шнура $l$ при различном числе подвешенных грузов. Прикрепляя резиновый шнур, следите, чтобы обе его части имели одинаковую длину. Для надежности крепления резинку несколько раз оберните вокруг каждой кнопки. Нитку завяжите петлей, прикрепите ее к верхней стороне линейки кнопкой, затем перебросьте ее через верхний край линейки. Все измерения проведите предельно аккуратно: изменяя число грузов, придерживайте линейку рукой, затем медленно ее опускайте или приподнимайте пока она не придет в состояние равновесия, старайтесь не допускать раскачивания грузов. Вы можете слегка передвигать нижний край линейки вдоль стенки для того, чтобы найти более устойчивое положение. Теоретическое описание

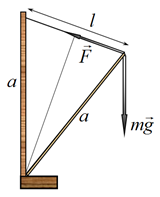
2.1. Покажите, что условием равновесия линейки при описанном способе крепления имеет вид $$F(l)=mg\frac{l}{a},\eqno(1)$$ где $l$ — длина шнура, $F(l)$ — сила упругости шнура при его длине $l$, $a$ — длина линейки, $mg$ — сила тяжести подвешенных грузов.
2.2. Используя данные, полученные в первой части, постройте на одном графике зависимости силы упругости от длины резинового шнура при нагрузке и разгрузке. При этом не забудьте, что начальная длина шнура в этой части у вас другая! На этом же бланке постройте графики функций $f(l)=mg\frac{l}{a}$ для шести возможных значений масс грузов.
2.3. С помощью построенных графиков найдите значения длины шнура $l$, соответствующие положениям равновесия при различных массах подвешенных грузов и в двух случаях, при нагрузке и при разгрузке. Постройте на одном графике зависимости длины шнура в положении равновесия от силы тяжести грузов при нагрузке (последовательном увеличении числа грузов) и при разгрузке (последовательном уменьшении числа грузов). Эксперимент
2.4. Проведите измерения зависимости длины шнура $l$ в положении равновесия от силы тяжести подвешенных грузов. Измерения проводите в двух направлениях: при нагрузке и при разгрузке.
2.5 На том же листе, на котором построен график рассчитанной вами в п. $2.3$ зависимости, постройте графики полученных вами экспериментальных зависимостей.
Часть 3. Бистабильность (3 балла).

Если нижний край линейки сместить от вертикальной стенки (см. рис. 3), то при некоторой длине резинового жгута и для некоторых масс грузов возможно существование двух устойчивых положений равновесия (бистабильность): одно при положении линейки близком к вертикальному, второе при положении близком к горизонтальному. В данной части вам необходимо определить условия, при которых возникает бистабильность. Можно показать (вам этого делать не надо!), что при небольшом смещении $\delta$ нижнего края линейки условие равновесия $(1)$ приближенно заменяется следующим условием $$F(l)=mg\frac{l-\delta}{a}.\eqno(2)$$
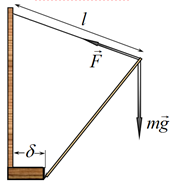
3.1. Схематически постройте на графике из п. $2.3$ такую функцию $f(l)=mg\frac{l-\delta}{a}$, которая описывает существование двух устойчивых положений равновесия, и укажите точками эти положения на графике. В функции $f(l)$ вы можете варьировать параметры $m$ и $\delta$ по своему желанию.
3.2. Длину свободной части резинки оставьте такой же, как в Части 2. Экспериментально исследуйте наличие двух устойчивых положений равновесия линейки при одном о том же количестве подвешенных грузов. Укажите, при каком числе подвешенных грузов существуют два положения устойчивого равновесия. Укажите длины резинок в этих положениях равновесия. Для поиска двух положений равновесия расположите сначала линейку почти вертикально и, аккуратное ее придерживая, дайте ей возможность медленно опускаться. Затем, растягивая шнур, приведите линейку в почти горизонтальное положение и, аккуратно придерживая рукой, дайте ей возможность медленно подниматься. Эту процедуру повторите несколько раз! При поиске бистабильности вы можете слегка изменять длину свободной части резинки. Если вы эту длину изменяли, то приведите ее новое значения (в сантиметрах).