7-я Жаутыковская олимпиада (2011), теоретический тур
(10 баллов)
Термодинамика простейшего квантового идеального газа В классической физике энергия системы изменяется непрерывно. В физике микромира большинство физических величин квантуется, то есть принимает дискретный ряд значений. Квантование энергии может приводить к реально наблюдаемым макроскопическим эффектам. В данной задаче вам предлагается рассмотреть простейшую модель квантового идеального газа. Модель
1 [1 балл] Определите число атомов $N_{n}$, имеющих энергию $E_{n}$. Ответ выразите через $N$, $\epsilon$, $T$ и $k_{B}$.
2. [3 балла] Найдите выражение для внутренней энергии $U$ газа. Ответ выразите через $N$, $\epsilon$, $T$ и $k_{B}$. Получите приближенные формулы для внутренней энергии газа в двух предельных случаях $k_{B}T\gg \epsilon$(высокая температура, классический предел) и $k_{B}T\ll \epsilon$ (предел низких температур).
3 [3 балла] Вычислите молярную теплоемкость газа $C_{\nu}$ при постоянном объеме. Ответ вы-разите через $N$, $\epsilon$, $T$ и $k_{B}$. Получите приближенные формулы для теплоемкости в классическом пределе и пределе низких температур. Постройте примерный график зависимости молярной теплоемкости рассматриваемого газа от температуры.
4 [3 балла] Найдите давление $P$, создаваемое газом на стенку сосуда. Ответ выразите через $N$, $\epsilon$, $T$ и $k_{B}$. Получите приближенные формулы для давления в классическом пределе и пределе низких температур. Постройте примерный график зависимости давления газа от температуры. При решении данных задач вы можете использовать формулы: $$\sum_{n=1}^{\infty} x^{n}=\frac{x}{1-x}$$ $$\sum_{n=1}^{\infty} n x^{n}=\frac{x}{(1-x)^2}$$ $$\exp(x)\thickapprox1+x, x\ll 1,$$ $$\frac{1}{1-x}\thickapprox 1+x, |x|\ll 1.$$
посмотреть в олимпиаде
Термодинамика простейшего квантового идеального газа В классической физике энергия системы изменяется непрерывно. В физике микромира большинство физических величин квантуется, то есть принимает дискретный ряд значений. Квантование энергии может приводить к реально наблюдаемым макроскопическим эффектам. В данной задаче вам предлагается рассмотреть простейшую модель квантового идеального газа. Модель
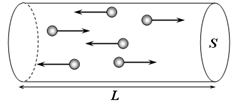
1 [1 балл] Определите число атомов $N_{n}$, имеющих энергию $E_{n}$. Ответ выразите через $N$, $\epsilon$, $T$ и $k_{B}$.
2. [3 балла] Найдите выражение для внутренней энергии $U$ газа. Ответ выразите через $N$, $\epsilon$, $T$ и $k_{B}$. Получите приближенные формулы для внутренней энергии газа в двух предельных случаях $k_{B}T\gg \epsilon$(высокая температура, классический предел) и $k_{B}T\ll \epsilon$ (предел низких температур).
3 [3 балла] Вычислите молярную теплоемкость газа $C_{\nu}$ при постоянном объеме. Ответ вы-разите через $N$, $\epsilon$, $T$ и $k_{B}$. Получите приближенные формулы для теплоемкости в классическом пределе и пределе низких температур. Постройте примерный график зависимости молярной теплоемкости рассматриваемого газа от температуры.
4 [3 балла] Найдите давление $P$, создаваемое газом на стенку сосуда. Ответ выразите через $N$, $\epsilon$, $T$ и $k_{B}$. Получите приближенные формулы для давления в классическом пределе и пределе низких температур. Постройте примерный график зависимости давления газа от температуры. При решении данных задач вы можете использовать формулы: $$\sum_{n=1}^{\infty} x^{n}=\frac{x}{1-x}$$ $$\sum_{n=1}^{\infty} n x^{n}=\frac{x}{(1-x)^2}$$ $$\exp(x)\thickapprox1+x, x\ll 1,$$ $$\frac{1}{1-x}\thickapprox 1+x, |x|\ll 1.$$
Комментарий/решение:
Возможно, что при неправильном наборе формул, они будут
доредактированы модератором. При этом содержание не будет меняться.