7-я Жаутыковская олимпиада (2011), теоретический тур
Электропроводность металлов (10 баллов)
Закон Ома
Проводниками называются материальные тела, в которых при наличии электрического поля возникает упорядоченное движение зарядов, то есть электрический ток. Закон, связывающий силу тока $I$, протекающего по проводнику, с разностью потенциалов (напряжением) $U$, приложенной к его концам, был открыт экспериментально Георгом Омом ($1787-1854$) и имеет вид $$I=\frac{U}{R},\eqno(1)$$
где $R$ — величина, называемая сопротивлением проводника.
Рассмотрим малый элемент проводника длиной $l$ и поперечным сечением $S$, к концам которого приложена разность потенциалов $U$. Пусть $\sigma$ — удельная электрическая проводимость вещества, которая является величиной, обратной удельному электрическому сопротивлению $\rho$. Электрическое сопротивление элемента проводника и сила тока, текущего по нему, равны $$R=\rho\frac{l}{S}=\frac{l}{\sigma S}, \hspace{5px} I=jS,\eqno(2)$$ где введена плотность тока $j$, представляющая собой количество заряда, проходящего в единицу времени через единицу поперечного сечения проводника и зависящая от концентрации электронов и их средней скорости упорядоченного движения.
Принимая во внимание, что $E=U/l$ — напряженность электрического поля, из $(1)$ и $(2)$ получаем локальную (дифференциальную) форму записи закона Ома $$j=\sigma E. \eqno(3)$$ Учитывая, что направления векторов напряженности электрического поля и плотности тока в проводнике одинаковы, это соотношение можно записать в векторном виде $$je\sigma E. \eqno(4)$$
1. [1 балл] Исходя из закона Джоуля-Ленца, впервые открытом Джеймсом Джоулем и позже Эмилем Ленцем, определите объемную плотность тепловой мощности $P_{V}$, выделяемой в проводнике, то есть теплоты, образующейся в 1 м$^3$ проводника за $1$ с. Ответ выразите через $E$ и $\sigma$.
Модель Друде
2. [1 балл] Определите вектор средней упорядоченной скорости движения электронов $u$. Ответ выразите через $e$, $E$, $m$ и $\tau$.
3. [1 балл] Плотность тока определяется компонентой средней скорости, параллельной вектору напряженности внешнего электрического поля $E$. Покажите, что в этой модели справедлив закон Ома и найдите проводимость металла $\sigma$. Ответ выразите через $e$, $n$, $m$ и $\tau$.
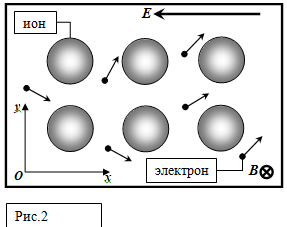
4. [1 балл] Какое количество теплоты $Q_{V}$ передают электроны кристаллической решетке в $1$ м$^3$ проводника за $1$ с. Ответ выразите через $e$, $E$, $n$, $m$ и $\tau$. Магнетосопротивление Важным гальваномагнитным явлением является изменение проводимости проводника, помещенного в поперечное магнитное поле. Это явление называется эффектом магнетосопротивления. Как показывает опыт, относительное изменение удельной проводимости $\Delta \sigma /\sigma$ при не очень сильных магнитных полях с индукцией $B$ выражается формулой $$\frac{\Delta \sigma}{\sigma}=\frac{\sigma (B)-\sigma(B=0)}{\sigma (B=0)=\mu B^{\nu}}, \eqno(5)$$ где $\mu$ и $\nu$ — некоторые постоянные. Используя модель Друде, описанную выше, выполните следующие задания. Внимательно изучите второй рисунок $2$, представленный выше, так как на нем представлены система координат и направления всех векторов.
5. [1 балл] Найдите зависимости проекций скорости электрона на оси координат $u_{x}(t)$ и $u_{y}(t)$ от времени $t$ между двумя последовательными столкновениями. Ответ выразите через $e$, $E$, $B$, $m$ и $t$.
6. [2 балла] Плотность тока определяется компонентой средней скорости, параллельной вектору напряженности внешнего электрического поля $E$. Считая величину индукции магнитного поля $B$ достаточно малой, определите значения постоянных $\mu$ и $\nu$ в формуле (5). Ответ выразите через $e$, $m$ и $r$.
Эффект Холла Эдвин Холл в $1879$ году открыл явление возникновения поперечной разности потенциалов, называемой холловским напряжением, при помещении проводника с током в постоянное магнитное поле. В простейшем рассмотрении эффект Холла выглядит следующим образом. Пусть через металлический брус в слабом магнитном поле $B$ течёт электрический ток под действием напряжённости внешнего электрического поля $E$. Магнитное поле будет отклонять электроны от их прямолинейного движения к одной из граней бруса. Таким образом, сила Лоренца приведёт, в отличие от магнетосопротивления, к накоплению отрицательного заряда возле одной грани бруска и положительного — возле противоположной. Накопление заряда будет продолжаться до тех пор, пока возникшее поперечное электрическое поле зарядов $E_{H}$ (направленное на представленном выше рисунке вдоль оси $O_{y}$) полностью не скомпенсирует за время $\tau$ поперечное смещение электронов. Используя модель Друде, описанную выше, выполните следующие задания. Внимательно изучите рисунок $2$, представленный выше, так как на нем представлены система координат и направления всех векторов.
7. [0.5 балла] Внимательно посмотрите на второй рисунок, приведенный выше. Возле какой из граней, верхней или нижней, будет происходить накопление отрицательного заряда?
8. [1.5 балла] Найдите зависимости проекций скорости электрона на оси координат $u_{x}(t)$ и $u_{y}(t)$ от времени $t$ между двумя столкновениями. Ответ выразите через $e$, $E$, $E_{H}$, $B$, $m$ и $t$.
9. [1 балл] Найдите холловскую напряженность поперечного электрического поля $E_{H}$. Ответ выразите через $e$, $E$, $B$, $m$ и $\tau$, а затем через $e$, $j$, $B$ и $n$. При решении данной задачи вы можете использовать приближенные формулы, справедливые при малых значениях $x$:$$\sin x\thickapprox x-\frac{x^3}{6}$$ $$\cos x\thickapprox 1-\frac{x^2}{2}+\frac{x^4}{24}$$
посмотреть в олимпиаде
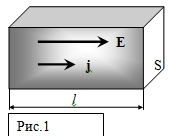
Рассмотрим малый элемент проводника длиной $l$ и поперечным сечением $S$, к концам которого приложена разность потенциалов $U$. Пусть $\sigma$ — удельная электрическая проводимость вещества, которая является величиной, обратной удельному электрическому сопротивлению $\rho$. Электрическое сопротивление элемента проводника и сила тока, текущего по нему, равны $$R=\rho\frac{l}{S}=\frac{l}{\sigma S}, \hspace{5px} I=jS,\eqno(2)$$ где введена плотность тока $j$, представляющая собой количество заряда, проходящего в единицу времени через единицу поперечного сечения проводника и зависящая от концентрации электронов и их средней скорости упорядоченного движения.
Принимая во внимание, что $E=U/l$ — напряженность электрического поля, из $(1)$ и $(2)$ получаем локальную (дифференциальную) форму записи закона Ома $$j=\sigma E. \eqno(3)$$ Учитывая, что направления векторов напряженности электрического поля и плотности тока в проводнике одинаковы, это соотношение можно записать в векторном виде $$je\sigma E. \eqno(4)$$
1. [1 балл] Исходя из закона Джоуля-Ленца, впервые открытом Джеймсом Джоулем и позже Эмилем Ленцем, определите объемную плотность тепловой мощности $P_{V}$, выделяемой в проводнике, то есть теплоты, образующейся в 1 м$^3$ проводника за $1$ с. Ответ выразите через $E$ и $\sigma$.
Модель Друде
2. [1 балл] Определите вектор средней упорядоченной скорости движения электронов $u$. Ответ выразите через $e$, $E$, $m$ и $\tau$.
3. [1 балл] Плотность тока определяется компонентой средней скорости, параллельной вектору напряженности внешнего электрического поля $E$. Покажите, что в этой модели справедлив закон Ома и найдите проводимость металла $\sigma$. Ответ выразите через $e$, $n$, $m$ и $\tau$.
4. [1 балл] Какое количество теплоты $Q_{V}$ передают электроны кристаллической решетке в $1$ м$^3$ проводника за $1$ с. Ответ выразите через $e$, $E$, $n$, $m$ и $\tau$. Магнетосопротивление Важным гальваномагнитным явлением является изменение проводимости проводника, помещенного в поперечное магнитное поле. Это явление называется эффектом магнетосопротивления. Как показывает опыт, относительное изменение удельной проводимости $\Delta \sigma /\sigma$ при не очень сильных магнитных полях с индукцией $B$ выражается формулой $$\frac{\Delta \sigma}{\sigma}=\frac{\sigma (B)-\sigma(B=0)}{\sigma (B=0)=\mu B^{\nu}}, \eqno(5)$$ где $\mu$ и $\nu$ — некоторые постоянные. Используя модель Друде, описанную выше, выполните следующие задания. Внимательно изучите второй рисунок $2$, представленный выше, так как на нем представлены система координат и направления всех векторов.
5. [1 балл] Найдите зависимости проекций скорости электрона на оси координат $u_{x}(t)$ и $u_{y}(t)$ от времени $t$ между двумя последовательными столкновениями. Ответ выразите через $e$, $E$, $B$, $m$ и $t$.
6. [2 балла] Плотность тока определяется компонентой средней скорости, параллельной вектору напряженности внешнего электрического поля $E$. Считая величину индукции магнитного поля $B$ достаточно малой, определите значения постоянных $\mu$ и $\nu$ в формуле (5). Ответ выразите через $e$, $m$ и $r$.
Эффект Холла Эдвин Холл в $1879$ году открыл явление возникновения поперечной разности потенциалов, называемой холловским напряжением, при помещении проводника с током в постоянное магнитное поле. В простейшем рассмотрении эффект Холла выглядит следующим образом. Пусть через металлический брус в слабом магнитном поле $B$ течёт электрический ток под действием напряжённости внешнего электрического поля $E$. Магнитное поле будет отклонять электроны от их прямолинейного движения к одной из граней бруса. Таким образом, сила Лоренца приведёт, в отличие от магнетосопротивления, к накоплению отрицательного заряда возле одной грани бруска и положительного — возле противоположной. Накопление заряда будет продолжаться до тех пор, пока возникшее поперечное электрическое поле зарядов $E_{H}$ (направленное на представленном выше рисунке вдоль оси $O_{y}$) полностью не скомпенсирует за время $\tau$ поперечное смещение электронов. Используя модель Друде, описанную выше, выполните следующие задания. Внимательно изучите рисунок $2$, представленный выше, так как на нем представлены система координат и направления всех векторов.
7. [0.5 балла] Внимательно посмотрите на второй рисунок, приведенный выше. Возле какой из граней, верхней или нижней, будет происходить накопление отрицательного заряда?
8. [1.5 балла] Найдите зависимости проекций скорости электрона на оси координат $u_{x}(t)$ и $u_{y}(t)$ от времени $t$ между двумя столкновениями. Ответ выразите через $e$, $E$, $E_{H}$, $B$, $m$ и $t$.
9. [1 балл] Найдите холловскую напряженность поперечного электрического поля $E_{H}$. Ответ выразите через $e$, $E$, $B$, $m$ и $\tau$, а затем через $e$, $j$, $B$ и $n$. При решении данной задачи вы можете использовать приближенные формулы, справедливые при малых значениях $x$:$$\sin x\thickapprox x-\frac{x^3}{6}$$ $$\cos x\thickapprox 1-\frac{x^2}{2}+\frac{x^4}{24}$$
Комментарий/решение:
Возможно, что при неправильном наборе формул, они будут
доредактированы модератором. При этом содержание не будет меняться.