5-я Жаутыковская олимпиада (2009), теоретический тур
Электромагнитные качели (10 баллов)
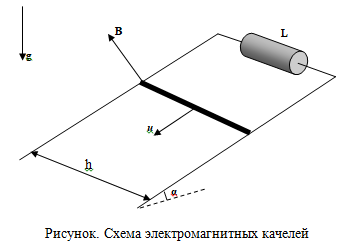
Два длинных проводящих стержня, соединённых вверху катушкой с индуктивностью $L$, образуют наклонную плоскость, составляющую угол $\alpha$ с горизонтом. Подвижный про-водник массой $m$ (см. рис.) способен скользить по стержням, всё время оставаясь перпендикулярным к ним и сохраняя с ними хороший электрический контакт. Коэффициент трения скольжения между проводником и стержнями равен $\mu$, расстояние между стержнями равно $g$, ускорение свободного падения равно $g$. Вся система помещена в перпендикулярное наклонной плоскости однородное магнитное поле с индукцией $B$. В данной задаче полностью пренебрегается омическим сопротивлением и индуктивностью стержней и проводника. Считая, что в начальный момент времени проводник покоится, а затем без толчка освобождается, дайте ответы на следующие вопросы.
посмотреть в олимпиаде
Два длинных проводящих стержня, соединённых вверху катушкой с индуктивностью $L$, образуют наклонную плоскость, составляющую угол $\alpha$ с горизонтом. Подвижный про-водник массой $m$ (см. рис.) способен скользить по стержням, всё время оставаясь перпендикулярным к ним и сохраняя с ними хороший электрический контакт. Коэффициент трения скольжения между проводником и стержнями равен $\mu$, расстояние между стержнями равно $g$, ускорение свободного падения равно $g$. Вся система помещена в перпендикулярное наклонной плоскости однородное магнитное поле с индукцией $B$. В данной задаче полностью пренебрегается омическим сопротивлением и индуктивностью стержней и проводника. Считая, что в начальный момент времени проводник покоится, а затем без толчка освобождается, дайте ответы на следующие вопросы.
- Запишите неравенство, при выполнении которого проводник начнёт свое движение вниз после отпускания. Ответ выразите через $\alpha$, $\mu$; (1 балл)
- Считая, что условия вопроса $1$ выполнены и проводник начал движение вниз, найдите зависимость силы тока $I$ в катушке индуктивности от смещения $x$ проводника от начального положения. Ответ выразите через $h$, $B$, $L$, $x$; (2 балла)
- Найдите максимальную скорость проводника $u_{\max}$ в процессе его движения. Ответ выразите через $h$, $B$, $L$, $m$, $\alpha$, $g$, $\mu$; (1 балл)
- Найдите максимальную силу тока $I_{\max}$ в катушке индуктивности в процессе движения проводника. Ответ выразите через $h$, $B$, $m$, $\alpha$, $g$, $\mu$; (1 балл)
- Вычислите количество выделившейся из-за трения теплоты за очень большое время в случае малой силы трения. Ответ выразите через $h$, $B$, $L$, $m$, $\alpha$, $g$; (3 балла)
- Какова относительная ошибка ответа предыдущего пункта в случае $\mu=\frac{tg \alpha}{2009}$? (2 балла)
Комментарий/решение:
Возможно, что при неправильном наборе формул, они будут
доредактированы модератором. При этом содержание не будет меняться.