Областная олимпиада по физике 2012, 11 класс, теоретический тур

Катушка индуктивностью 10$^{-3}$ Гн соединена параллельно с резистором $R$, электрическое сопротивление которого равно 1 кОм. Активное сопротивление катушки пренебрежимо мало. Катушка и резистор подключаются к источнику тока с ЭДС 10 В и внутренним сопротивлением $r$, равным 10 Ом. Какой заряд протечет через резистор $R$ за 1 секунду (рис.1)? (8 баллов)

Комментарий/решение

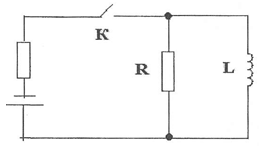
В данной схеме реализуется переходный процесс . Значит, ток через резистор будет меняться, и заряд придётся находить интегрированием : $q=\int \limits_{0}^{1}{I(t)dt}$. В верхнем пределе стоит единица, потому что нас интересует заряд в течении $1$ секунды. Применим классический метод расчёта переходных процессов. Закон изменения тока будем искать в виде $I(t)=I_{пр}+I_{св}(t)$ . Здесь $I_{пр}$- приведенная составляющая тока через резистор (при $t\to \infty$); $I_{св}(t)$-свободная составляющая. При $t\to \infty$ катушку заменим перемычкой . Ток потечет по перемычке (так как ее активное сопротивление $0$ ), значит, $I_{пр}=0$. Далее стоит применить закон коммутации: ток на катушке не может после коммутации (замыкания ключа) измениться скачком. Отсюда $I_L(0-)=I_L(0+)$. Здесь $I_L(0-)$ и $I_L(0+)$- значения тока на катушке до коммутации и сразу после. Ясно, что $I_L(0-)=0$. Это потому, что до коммутации цепь разомкнута. Значит, $I_L(0+)=0$. Теперь рассмотрим цепь сразу после включения . Из схемы можно убрать ветку с катушкой, так как через нее не течет ток. Ток на резисторе в момент $t\to 0+$:$I(0+)=\dfrac{E}{r+R}$. Свободную составляющую тока найдём в виде $I_{св}=A\cdot{e^{pt}}$. Используем граничные условия, найдём $A$ $$I(0+)=I_{пр}+I_{св}(t)=0+A\cdot{e^{0}}=A=\dfrac{E}{r+R}$$ Осталось найти константу $p$ . Для этого заменим в схеме катушку на резистор с сопротивлением $pL$ и найдем сопротивление входа $Z(p)$ (через зажимы эдс), приравняем его нулю $$Z(p)=r+\dfrac{R\cdot{pL}}{R+pL}=0$$ Отсюда $p=-\dfrac{rR}{L\cdot{(r+R)}}$ Всё. Теперь можно приступить к интегрированию. $$q=\int \limits_{0}^{1}{\dfrac{E}{r+R}\cdot{e^{-\dfrac{rRt}{L\cdot{(r+R)}}}}dt}=\dfrac{EL}{Rr}\cdot{(1-e^{-\dfrac{rR}{L\cdot{(r+R)}}})}=6,21\cdot{10^{-10}} Кл$$