Геометриядан Иран олимпиадасы, 2017 жыл, 1-ші лига (7-8 сыныптар)

Төменгі суретте $ABC$ үшбұрышының бұрыштарын табыңыздар.

Комментарий/решение

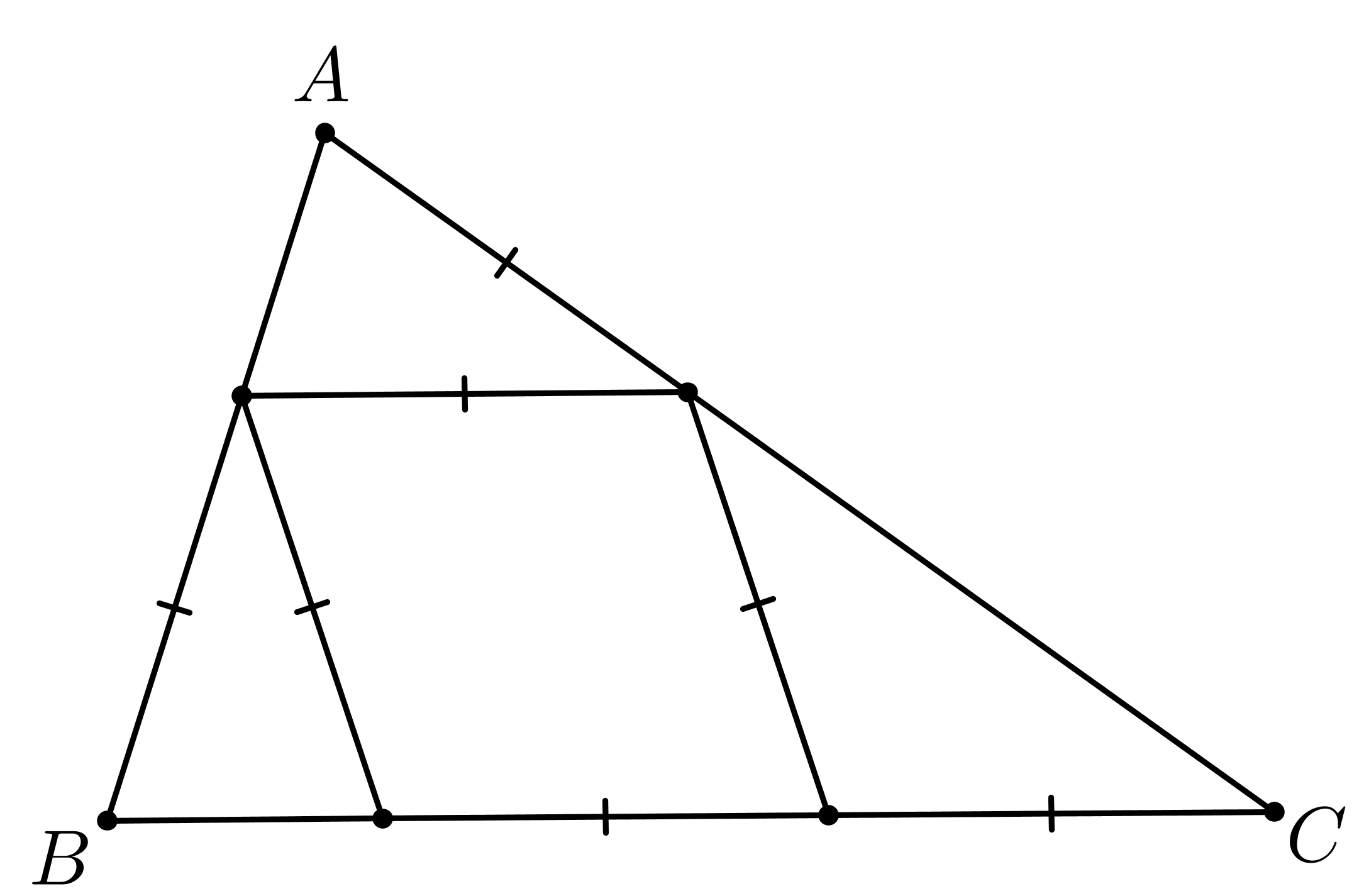
Фигура внутри треугольника ABC -ромб так как стороны равны.То диагонали ромба перпендикулярный.Обозначим вершины ромба MNKL.где M,N,P,K лежит на сторанах AB,AC,BC соответственно.Угол NPK=PNK=NPM=PNM=a,то угол NKC=2a,то углы KNS=KCN=90-a так как треугольник NKC равнобедренный.Тогда угол ANM =90-a,так как угол ANP=PNC=90 и угол MNP=PNK=a.Угол MPB=180-уголMPK=180-2a=угол MBPТо уголугол AMN=MAN=180-2a.Сумма внутренных углов треугольника AMN 2*(180-2a)+90-a=180,то a=54и углы треугольника ABC равен 72°,72°,36°.точнее угол ABC=72°,BAC72°,ACB=36°

Ответ: $\angle B=\angle A=72^\circ , \angle C=36^\circ$

Решение : Отметим вершины ромба, как $M,N,K,L(M \in AB, N \in AC, K,L \in BC).$

$\angle AMN=\angle ABC=\angle NKL=\angle KMN \Rightarrow \angle B =\angle C$

$\angle MLK=\angle MNK=\angle NKC \Rightarrow \angle B=\angle A=2\angle C \Leftrightarrow 5\alpha=180^\circ , \alpha=36^\circ$

$\angle A=\angle B =72^\circ , \angle C=36^\circ$