Геометриядан Иран олимпиадасы, 2017 жыл, 1-ші лига (7-8 сыныптар)

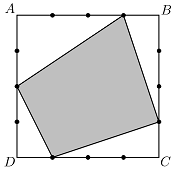
Қабырғасы 4 болатын $ABCD$ шаршысының әр қабырғасы үш нүктемен төрт тең кесіндіге бөлінген (төменгі сур. қара). Квадраттың әр қабырғасынан белгіленген төрт нүктенің біреуін таңдап алған. Таңдап алынған нүктелерді тізбектеп төртбұрыш шығатындай қосқан. Сол төртбұрыштың ауданы неге тең болуы мүмкін? Барлық мүмкін жауапты жазыңыздар, жауаптарды негіздеудің қажеті жоқ.

Комментарий/решение

Стороны квадрата равны 4 и каждая сторана поделена на четыре равные части.То длина между точек равен единичку.Площадь квадрат равен 4*4=16.Площадь черного четырехугольника равен разность площадьи квадрата и площади треугольников.Площади треугольника равен 3*2/2+3*1/2+3*1/2+2*1/2=7 то площадь чёрного квадрата равен 16-7=9

Это можно найти по формуле Пика.

S=В+Г/2-1, где В=8 Г=4.