Геометриядан Иран олимпиадасы, 2016 жыл, 3-ші лига (11-12 сыныптар)

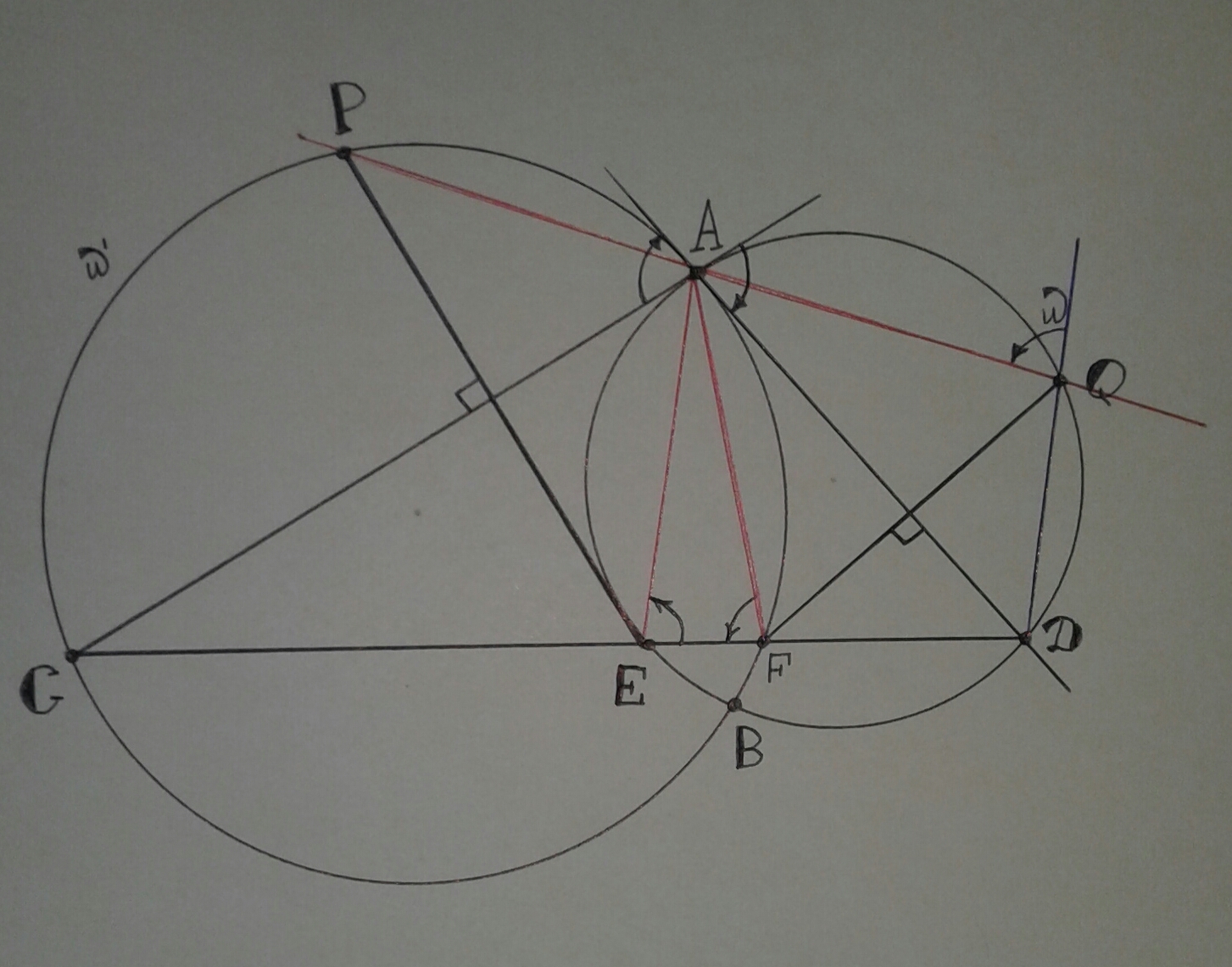
$\omega$ және $\omega'$ шеңберлері $A$ және $B$ нүктелерінде қиылысады. $\omega$-ға $A$ нүктесінде жүргізілген жанама $\omega'$-ты $C$ нүктесінде, ал $\omega'$-ке $A$ нүктесінде жүргізілген жанама $\omega$-ны $D$ нүктесінде қияды. $CD$ түзуі $\omega$ мен $\omega'$-ты сәйкесінше $E$ және $F$ нүктелерінде қисын ($E$ нүктесі $F$ пен $C$ арасында). $AC$ түзуіне $E$ нүктесінен түсірілген перпендикуляр $\omega'$-ты $P$ нүктесінде, ал $AD$ түзуіне $F$ нүктесінен түсірілген перпендикуляр $\omega$-ны $Q$ нүктесінде қияды ($A$, $P$ және $Q$ нүктелері $CD$ түзуінің бір жағында жатыр). $A$, $P$ және $Q$ нүктелері бір түзудің бойында жатқанын дәлелдеңіздер.

Комментарий/решение

$$\angle AFC + \angle CAD= \pi \Rightarrow \angle AFC= \pi - \angle CAD= \angle AED$$

$$\angle AEF + \angle AQD=\pi \Rightarrow \angle AEF= \pi - AQD$$

$$\Rightarrow \angle AFD= \angle AQD$$

$$\angle DAQ = \angle ACD =\angle DAF$$

$$\angle CAP =\angle CAE= \angle CDA \Rightarrow$$

$$\Rightarrow \angle ACD +\angle CAD + \angle CDA= \angle DAQ +\angle CAD +\angle CAP = \pi$$

$$\Rightarrow A,P,Q \in l$$