3-я международная Иранская олимпиада по геометрии, 2016 год, третья лига, 11-12 классы

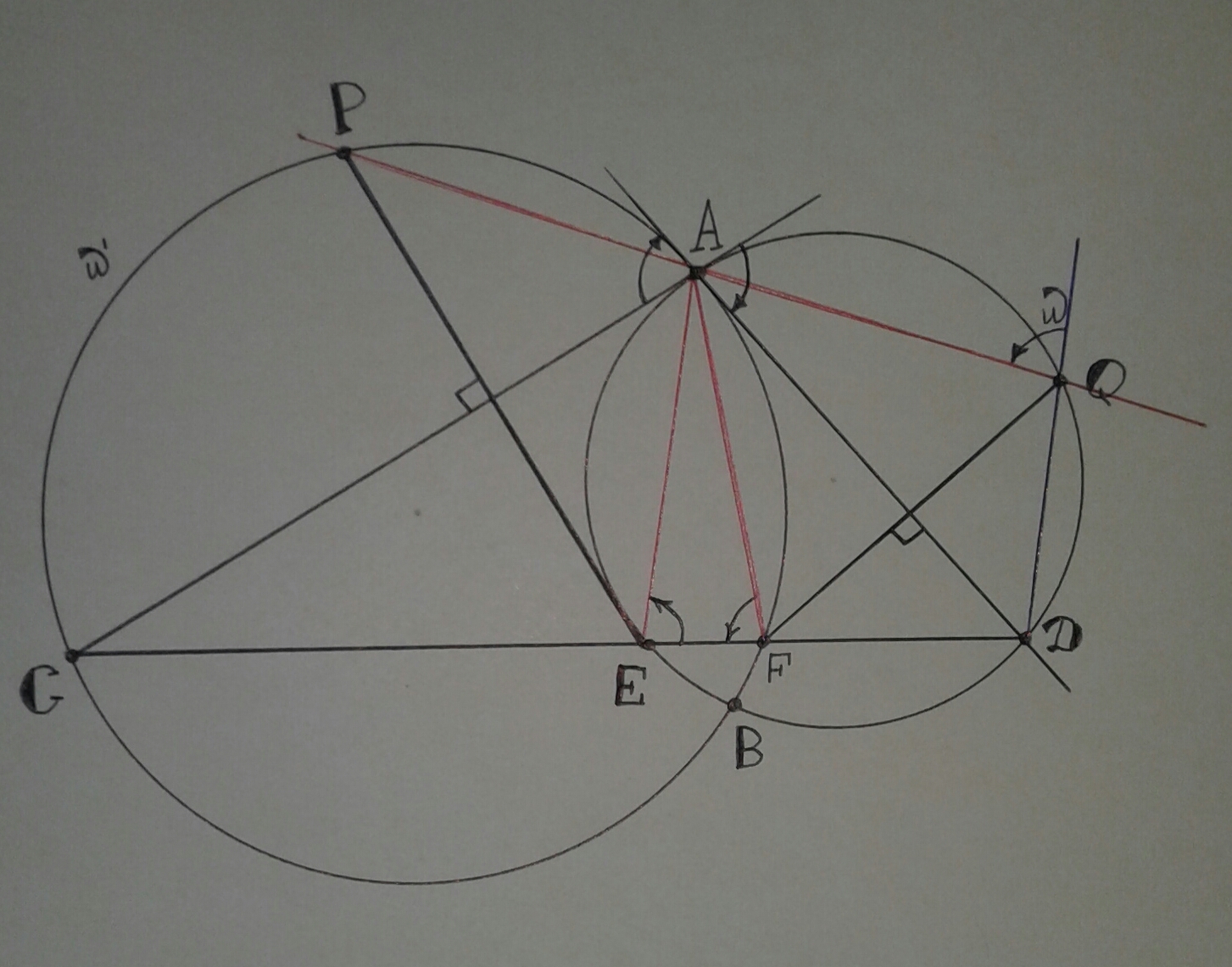
Окружности $\omega$ и $\omega'$ пересекаются в точках $A$ и $B$. Касательная к окружности $\omega$, проходящая через точку $A$, пересекает окружность $\omega'$ в точке $C$. Касательная к окружности $\omega'$, проходящая через $A$, пересекает $\omega$ в точке $D$. Прямая $CD$ пересекает окружности $\omega$ и $\omega'$ в точках $E$ и $F$ соответственно. Перпендикуляр из точки $E$ к прямой $AC$ пересекает $\omega'$ в точке $P$; перпендикуляр из точки $F$ к прямой $AD$ пересекает $\omega$ в точке $Q$; Точки $A$, $P$ и $Q$ лежат по одну сторону от прямой $CD$. Докажите, что точки $A$, $P$ и $Q$ лежат на одной прямой.

Комментарий/решение

$$\angle AFC + \angle CAD= \pi \Rightarrow \angle AFC= \pi - \angle CAD= \angle AED$$

$$\angle AEF + \angle AQD=\pi \Rightarrow \angle AEF= \pi - AQD$$

$$\Rightarrow \angle AFD= \angle AQD$$

$$\angle DAQ = \angle ACD =\angle DAF$$

$$\angle CAP =\angle CAE= \angle CDA \Rightarrow$$

$$\Rightarrow \angle ACD +\angle CAD + \angle CDA= \angle DAQ +\angle CAD +\angle CAP = \pi$$

$$\Rightarrow A,P,Q \in l$$