Районная олимпиада, 2004-2005 учебный год, 9 класс
Комментарий/решение:
1) Теорема: если для четырехугольника $WXYZ$ справедливы равенства
$$\overrightarrow{WX} = \overrightarrow{ZY};\;\;\overrightarrow{XY} = \overrightarrow{WZ};$$
то такой четырехугольник - параллелограмм
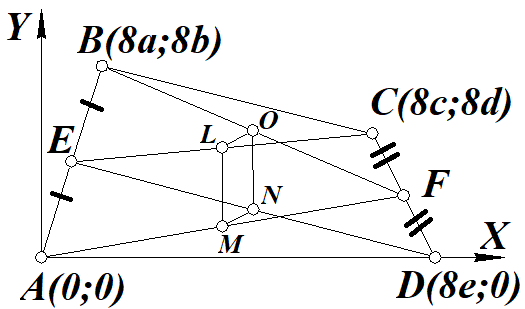
2) Введем систему координат:
$$A(0;0);B(8a;8b);C(8c;8d);D(8e;0)$$
Тогда
$$E\left(\dfrac{0+8a}{2};\dfrac{0+8b}{2}\right)\rightarrow E(4a;4b)$$
$$F\left(\dfrac{8c+8e}{2};\dfrac{8d+0}{2}\right)\rightarrow F(4c+4e;4d)$$
3) Пусть точка $L$ - середина $CE$
$$L\left(\dfrac{8c+4a}{2};\dfrac{8d+4b}{2}\right)\rightarrow L(4c+2a;4d+2b)$$
4) Пусть точка $M$ - середина $AF$
$$M\left(\dfrac{4c+4e+0}{2};\dfrac{4d+0}{2}\right)\rightarrow M(2c+2e;2d)$$
5) Пусть точка $N$ - середина $ED$
$$N\left(\dfrac{8e+4a}{2};\dfrac{0+4b}{2}\right)\rightarrow N(4e+2a;2b)$$
6) Пусть точка $O$ - середина $BF$
$$O\left(\dfrac{8a+4c+4e}{2};\dfrac{8b+4d}{2}\right)\rightarrow O(4a+2c+2e;4b+2d)$$
7) В задаче просят показать, что четырехугольник $LMNO - $ параллелограмм.
Это можно сделать по теореме (1)
$$\overrightarrow{LM} = (2c+2e-4c-2a;2d-4d-2b) = (-2c+2e-2a;-2d-2b)$$
$$\overrightarrow{ON} = (4e+2a-4a-2c-2e;2b-4b+2d) = (-2c+2e-2a;-2d-2b)$$
Понятно, что $$\overrightarrow{LM} = \overrightarrow{ON}$$
$$\overrightarrow{MN} = (4e+2a-2c-2e;2b-2d) = (2e+2a-2c;2b-2d)$$
$$\overrightarrow{LO} = (4a+2c+2e-4c-2a;4b+2d-4d-2b) = (2e+2a-2c;2b-2d)$$
Понятно, что $$\overrightarrow{MN} = \overrightarrow{LO}$$
То есть, $LMNO - $ параллелограмм.

Возможно, что при неправильном наборе формул, они будут
доредактированы модератором. При этом содержание не будет меняться.