Городская Жаутыковская олимпиада, 7 класс, 2008 год
Комментарий/решение:

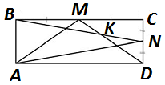
1) Угол $\angle MKB$ равен углу между векторами $\overrightarrow{NB}$ и $\overrightarrow{DM}$;угол $\angle MAN$ равен углу между векторами $\overrightarrow{AM}$ и $\overrightarrow{AN}$;
2) $\cos\angle MKB=\dfrac{\overrightarrow{NB}\cdot{\overrightarrow{DM}}}{|\overrightarrow{NB}|\cdot{|\overrightarrow{DM}|}}$; $\cos\angle MAN=\dfrac{\overrightarrow{AM}\cdot{\overrightarrow{AN}}}{|\overrightarrow{AM}|\cdot{|\overrightarrow{AN}|}}$
3) Находим координаты векторов
$\overrightarrow{NB}=(-2a;b);\overrightarrow{DM}=(-a;2b);\overrightarrow{AM}=(a;2b);\overrightarrow{AN}=(2a;b)$
4) $\overrightarrow{NB}\cdot{\overrightarrow{DM}}=-2a\cdot{(-a)}+b\cdot{2b}=2a^2+2b^2$
5)$\overrightarrow{AM}\cdot{\overrightarrow{AN}}=a\cdot{2a}+2b\cdot{b}=2a^2+2b^2$
6) $|\overrightarrow{NB}|=\sqrt{(-2a)^2+b^2}=\sqrt{4a^2+b^2}$
7) $|\overrightarrow{DM}|=\sqrt{(-a)^2+(2b)^2}=\sqrt{a^2+4b^2}$
8) $|\overrightarrow{AM}|=\sqrt{a^2+(2b)^2}=\sqrt{a^2+4b^2}$
9) $|\overrightarrow{AN}|=\sqrt{(2a)^2+b^2}=\sqrt{4a^2+b^2}$
10) $\cos\angle MKB=\dfrac{\overrightarrow{NB}\cdot{\overrightarrow{DM}}}{|\overrightarrow{NB}|\cdot{|\overrightarrow{DM}|}}=\dfrac{2a^2+2b^2}{\sqrt{4a^2+b^2}\sqrt{a^2+4b^2}}$;
$\cos\angle MAN=\dfrac{\overrightarrow{AM}\cdot{\overrightarrow{AN}}}{|\overrightarrow{AM}|\cdot{|\overrightarrow{AN}|}}=\dfrac{2a^2+2b^2}{\sqrt{4a^2+b^2}\sqrt{a^2+4b^2}}$
11) Из $[10]$ следует $\angle MKB=\angle MAN$
Возможно, что при неправильном наборе формул, они будут
доредактированы модератором. При этом содержание не будет меняться.