Городская Жаутыковская олимпиада, 8 класс, 2002 год

На сторонах $AD$ и $DC$ ромба $ABCD$ построены правильные треугольники $AKD$ и $DMC$ так, что точка $K$ лежит по ту же сторону от $AD$, что и прямая $BC$, а точка $M$ — по другую сторону от $DC$, чем $AB$. Докажите, что точки $B$, $K$ и $M$ лежат на одной прямой.

Комментарий/решение

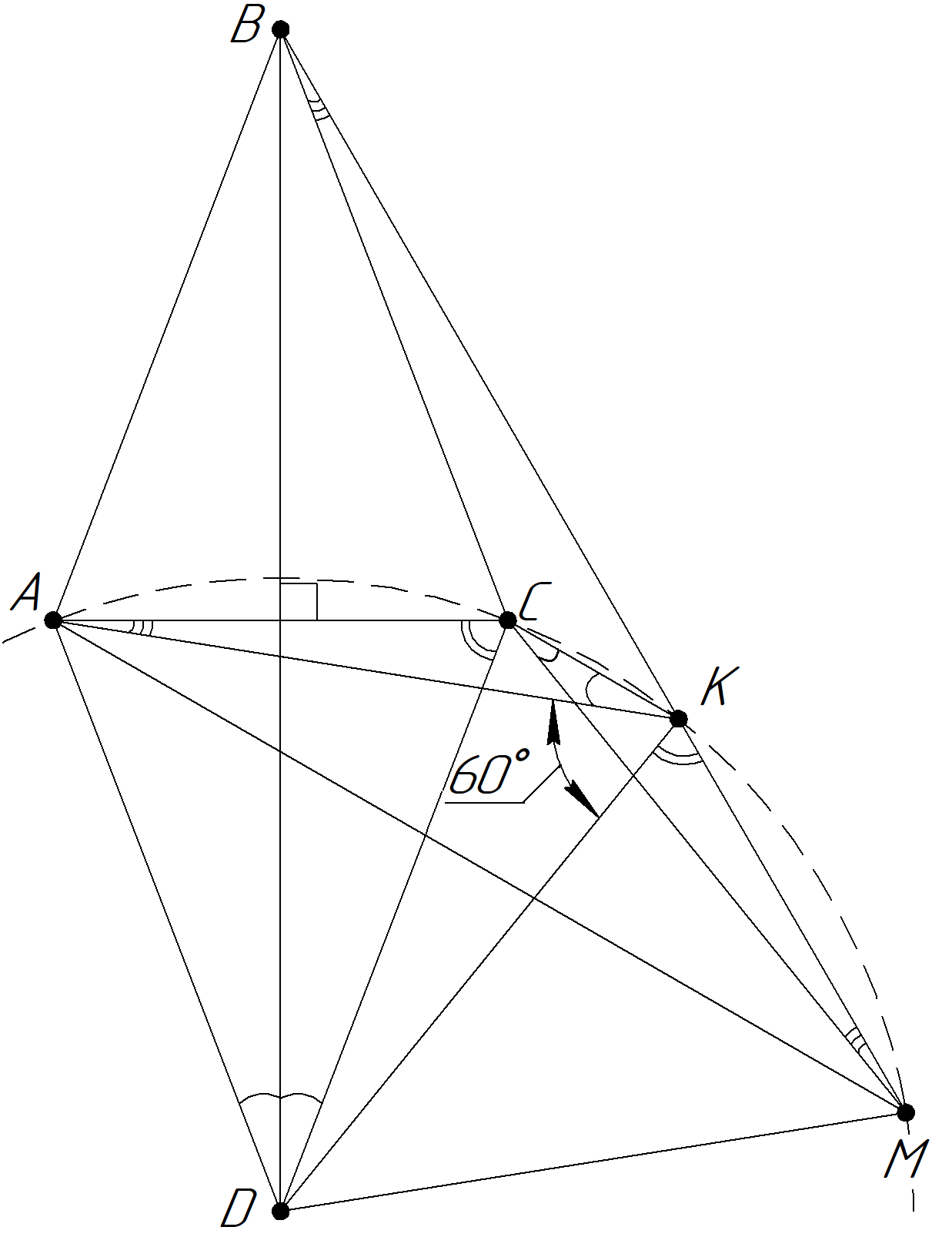
1)Четырёхугольник $ACKM$ вписан в окружность с центром в точке $D$

Доказательство. $\triangle DAK-$ равносторонний $\Rightarrow DA=DK$

$\triangle DCM-$ равносторонний $\Rightarrow DC=DM$

$DA=DC$ (свойство ромба, у него все стороны равны)

Обобщая, получаем $DA=DK=DC=DM=R$

2)$\angle ADB=\angle CDB=\dfrac{\angle ADC}{2}$ в силу того, что диагонали ромба являются биссектрисами

3) $\angle AKC$ и $\angle ADC$ опираются на дугу $\overset\frown{AC}$. Но $\angle ADC-$центральный. Поэтому $\angle AKC=\dfrac{\angle ADC}{2}=\angle ADB=\angle CDB$

4)$\angle DAC=\angle DCA;\angle DKM=\angle DMK$ (В силу равнобедренности треугольников $\triangle DAC,\triangle DKM$, это следует из $[1]$)

5)$\triangle ACD=\triangle DKM$

Доказательство. Из $[1]\Rightarrow DA=DK;DC=DM$

$\angle ADC=60^{\circ}-\angle CDK;\angle KDM=60^{\circ}-\angle CDK$

Получаем равенство по соответствующим двум сторонам и углу между ними.

6)Из $[4,5]\Rightarrow \angle ACD=\angle DKM$

7)$\angle AKD=60^{\circ}$ по условию

8)$\angle CKA+\angle DKM=\angle CDB+\angle DCA;$ так как $AC\bot DB$ (свойство диагоналей ромба), то $\angle CDB+\angle DCA=180^{\circ}-90^{\circ}=90^{\circ}$

9)Если $\angle MKB=180^{\circ}$, то утверждение задачи доказано. Выразим $\angle MKB$ через остальные углы

$\angle MKB=(\angle CKA+\angle DKM)+\angle AKD+\angle BKC=90^{\circ}+60^{\circ}+\angle BKC=150^{\circ}+\angle BKC$

10)$\triangle MCB-$равнобедренный

Доказательство.$DC=CM$ (из равностороннего $\triangle DCM$

$DC=CB$ (Из ромба $ABCD$)$\Rightarrow DC=CM=CB$

11) Из $[10]\Rightarrow \angle CMB=\angle CBM$

12)Рассмотрим $\triangle ACK$. Сумма углов в нем

$\angle CAK+\angle ACK+\angle CKA=\angle CAK+\angle ACD+\angle DCM+\angle MCK+\angle CKA=180^{\circ}$

Пусть $\angle CAK=x;\angle ACD=y;\angle AKC=z$

Тогда $x+y+60^{\circ}+z+z=180^{\circ}$ так как $y+z=90^{\circ}$, имеем $x+y=30^{\circ}$

13) Рассмотрим $\triangle ABK$. Сумма углов в нем

$x+y+z+z+x+\angle BKC+z=180^{\circ}$ Отсюда следует, что

$\angle BKC=x+y=30^{\circ}$

14)Подставим $[13]$ в $[9]$. Получим $\angle MKB=150^{\circ}+\angle BKC=150^{\circ}+30^{\circ}=180^{\circ}$. То есть $\angle MKB-$развёрнутый, то есть прямая, то есть точки $M,K,B$ лежат на одной прямой